Предмет: Алгебра,
автор: alpine347
Помогите с пределами
Приложения:
Ответы
Автор ответа:
0
4а) Неопределённость 0/0. Приводим к первому замечательному пределу:

4б) Тоже неопределённость 0/0. Приводим к первому замечательному пределу:


4в) Неопределённость . Приводим ко второму замечательному пределу:
. Приводим ко второму замечательному пределу:
![lim_{x to infty} (1+ frac{1}{2x} )^x=lim_{x to infty} [(1+ frac{1}{2x} )^{2x* frac{1}{2x} } ]^x= \ \ =lim_{x to infty} [(1+ frac{1}{2x} )^{2x} ]^{ frac{1}{2x} *x}=lim_{x to infty} [(1+ frac{1}{2x} )^{2x} ]^{ frac{1}{2}}=e^{frac{1}{2}} = sqrt{e} lim_{x to infty} (1+ frac{1}{2x} )^x=lim_{x to infty} [(1+ frac{1}{2x} )^{2x* frac{1}{2x} } ]^x= \ \ =lim_{x to infty} [(1+ frac{1}{2x} )^{2x} ]^{ frac{1}{2x} *x}=lim_{x to infty} [(1+ frac{1}{2x} )^{2x} ]^{ frac{1}{2}}=e^{frac{1}{2}} = sqrt{e}](https://tex.z-dn.net/?f=+lim_%7Bx+to+infty%7D+%281%2B++frac%7B1%7D%7B2x%7D+%29%5Ex%3Dlim_%7Bx+to+infty%7D+%5B%281%2B+frac%7B1%7D%7B2x%7D+%29%5E%7B2x%2A+frac%7B1%7D%7B2x%7D+%7D+%5D%5Ex%3D+%5C++%5C+%3Dlim_%7Bx+to+infty%7D+%5B%281%2B+frac%7B1%7D%7B2x%7D+%29%5E%7B2x%7D+%5D%5E%7B+frac%7B1%7D%7B2x%7D+%2Ax%7D%3Dlim_%7Bx+to+infty%7D+%5B%281%2B+frac%7B1%7D%7B2x%7D+%29%5E%7B2x%7D+%5D%5E%7B+frac%7B1%7D%7B2%7D%7D%3De%5E%7Bfrac%7B1%7D%7B2%7D%7D+%3D+sqrt%7Be%7D+)
4г) Неопределённость . Приводим ко второму замечательному пределу:
. Приводим ко второму замечательному пределу:
![lim_{x to inft0} (1-2x )^{ frac{1}{x} }=lim_{x to inft0} (1+(-2x) )^{ frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}* (-2x) } ]^{ frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}} ]^{ (-2x)* frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}} ]^{ -2 }=e^{-2} lim_{x to inft0} (1-2x )^{ frac{1}{x} }=lim_{x to inft0} (1+(-2x) )^{ frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}* (-2x) } ]^{ frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}} ]^{ (-2x)* frac{1}{x} }= \ \ =lim_{x to inft0} [(1+(-2x) )^{ frac{1}{-2x}} ]^{ -2 }=e^{-2}](https://tex.z-dn.net/?f=+lim_%7Bx+to+inft0%7D+%281-2x+%29%5E%7B+frac%7B1%7D%7Bx%7D+%7D%3Dlim_%7Bx+to+inft0%7D+%281%2B%28-2x%29+%29%5E%7B+frac%7B1%7D%7Bx%7D+%7D%3D+%5C++%5C+%3Dlim_%7Bx+to+inft0%7D+%5B%281%2B%28-2x%29+%29%5E%7B+frac%7B1%7D%7B-2x%7D%2A+%28-2x%29+%7D+%5D%5E%7B+frac%7B1%7D%7Bx%7D+%7D%3D+%5C++%5C++%3Dlim_%7Bx+to+inft0%7D+%5B%281%2B%28-2x%29+%29%5E%7B+frac%7B1%7D%7B-2x%7D%7D+%5D%5E%7B+%28-2x%29%2A+frac%7B1%7D%7Bx%7D+%7D%3D+%5C++%5C+%3Dlim_%7Bx+to+inft0%7D+%5B%281%2B%28-2x%29+%29%5E%7B+frac%7B1%7D%7B-2x%7D%7D+%5D%5E%7B+-2+%7D%3De%5E%7B-2%7D)
4б) Тоже неопределённость 0/0. Приводим к первому замечательному пределу:
4в) Неопределённость
4г) Неопределённость
Автор ответа:
0
task/26096452
--------------------
см приложения
--------------------
см приложения
Приложения:
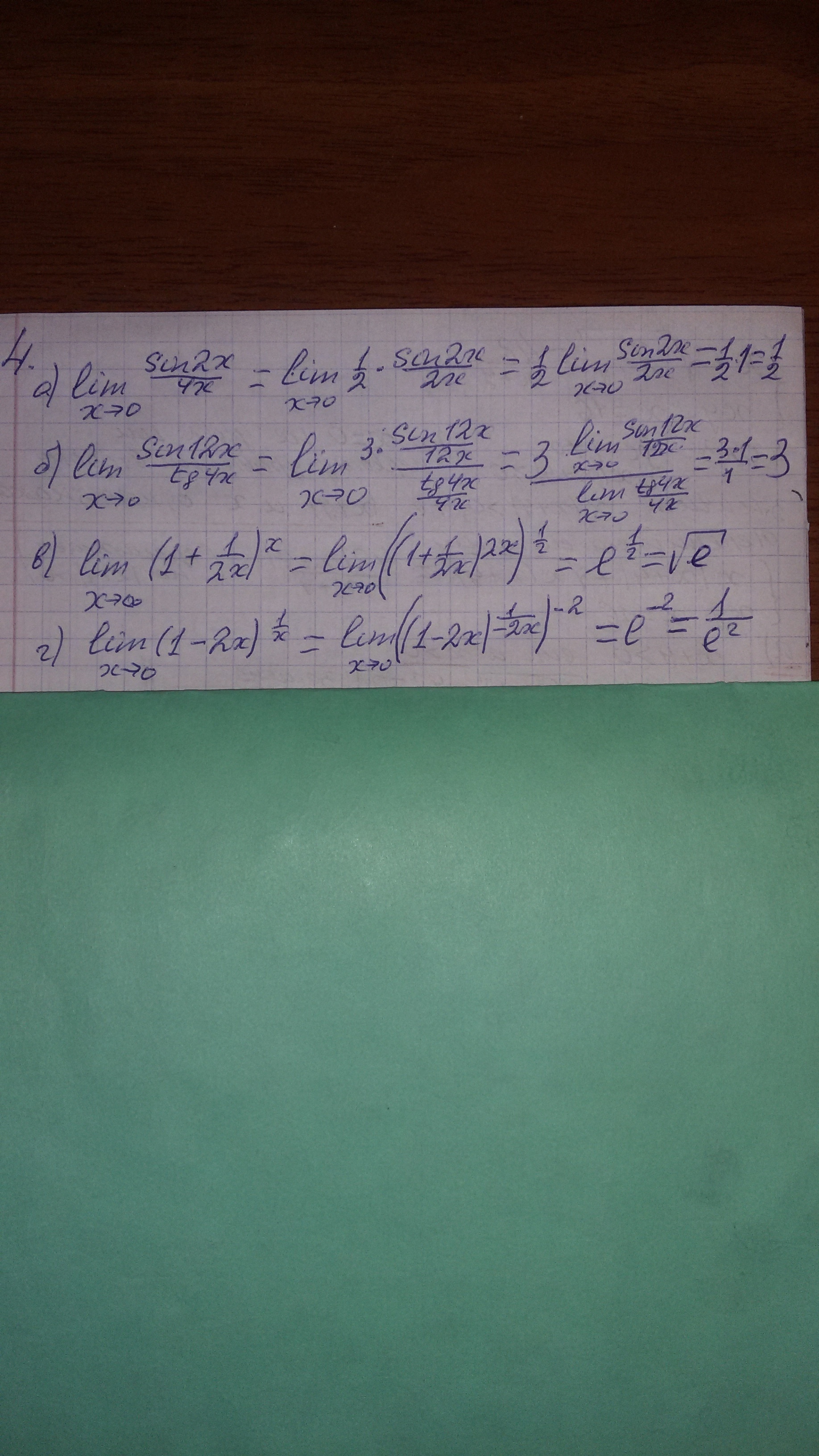
Похожие вопросы
Предмет: Алгебра,
автор: Flowie
Предмет: Английский язык,
автор: eababayan2009
Предмет: Қазақ тiлi,
автор: firuza2287
Предмет: Химия,
автор: OrtodoX
Предмет: Алгебра,
автор: Krisloran1