Предмет: Алгебра,
автор: Маришка20171
ПОМОГИТЕ ПОЖАЛУСТА. У МЕНЯ НЕ ПОЛУЧАЕТСЯ НОМЕР 7. ПОЖАЛУЙСТА! !!
Приложения:

Ответы
Автор ответа:
0
1) область опеделения: х≠-5, х∈(-∞;-5)∪(-5;+∞)
Область допустимых значений y∈(-∞;+∞)
2)
Функция не является ни четной, ни нечетной
3)Точки пересечения с осями
y(0)=1/5=0,2

(0;0,2) и (-0,5;0)
4) Асимптоты функции.

В точке х=-5 функция терпит разрыв
5) Экстремумы и интервалы монотонности

y'≠0, функция монотонно возрастает на интервалах (-∞;-5) и (-5;+∞)
6) Точки перегиба и промежутки выпуклости, вогнутости.

На промежутке (-∞;-5) функция выпукла вниз так как y''>0
На промежутке (-5;+∞) функция выпукла вверх так как y''<0
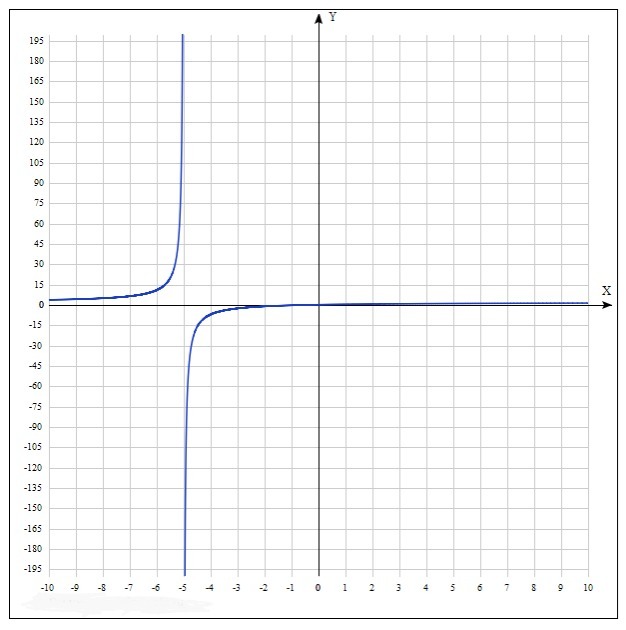
7) График на картинке
Область допустимых значений y∈(-∞;+∞)
2)
Функция не является ни четной, ни нечетной
3)Точки пересечения с осями
y(0)=1/5=0,2
(0;0,2) и (-0,5;0)
4) Асимптоты функции.
В точке х=-5 функция терпит разрыв
5) Экстремумы и интервалы монотонности
y'≠0, функция монотонно возрастает на интервалах (-∞;-5) и (-5;+∞)
6) Точки перегиба и промежутки выпуклости, вогнутости.
На промежутке (-∞;-5) функция выпукла вниз так как y''>0
На промежутке (-5;+∞) функция выпукла вверх так как y''<0
7) График на картинке
Приложения:
Похожие вопросы
Предмет: Математика,
автор: limanskajoksana092
Предмет: Окружающий мир,
автор: zylia8484
Предмет: Геометрия,
автор: supertaaaazik
Предмет: Алгебра,
автор: dan4sslash
Предмет: Литература,
автор: vuz08