Предмет: Геометрия,
автор: sovyshka2001
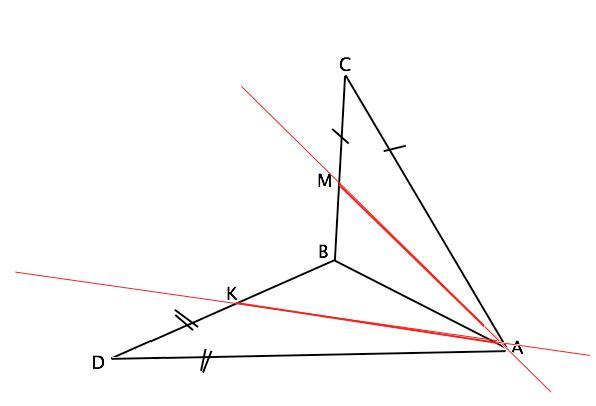
Два равнобедренных треугольника ABC и ABD с общим основанием AB расположены так, что точка C не лежит в плоскости ABD. Определите взаимное расположение прямых, содержащих медианы треугольника, проведённых к сторонам BC и BD.
1) они параллельны; 2) скрещваются; 3) пересекаются
МОЖНО ОТВЕТ С РЕШЕНИЕМ, ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО!
Ответы
Автор ответа:
0
Ответ: Данные прямые пересекаются.
Объяснение:
Пусть К - середина BD, М - середина ВС.
Прямые АК и АМ имеют ОДНУ общую точку А. Следовательно, они пересекаются, т.к. параллельные и скрещивающиеся прямые общих точек не имеют.
Приложения:
Похожие вопросы
Предмет: История,
автор: sofiaroblox93
Предмет: Математика,
автор: nikolaevamilana08
Предмет: Алгебра,
автор: subinad93
Предмет: Математика,
автор: katrin892094