Question

В треугольнике ABC AC = 6, высота BH = 6 ( Точка H лежит на отрезке AC), AH=2HC, M - середина AB, Р - середина BC. Точки К и Т лежат на стороне АС так, что углы KMP и MPT - прямые. Отрезки AP и BH пересекаются в точке Q
Найдите:
a) длину отрезка МК
б) величину угла между прямыми KP и MT
в) отношение AQ : QP

ДАЮ 75 БАЛЛОВ, СРОЧНО

С объяснением и рисунком позяяяя :) ( Насколько я знаю, через т.Фалеса надо делать, но это не точно)

Answer 1

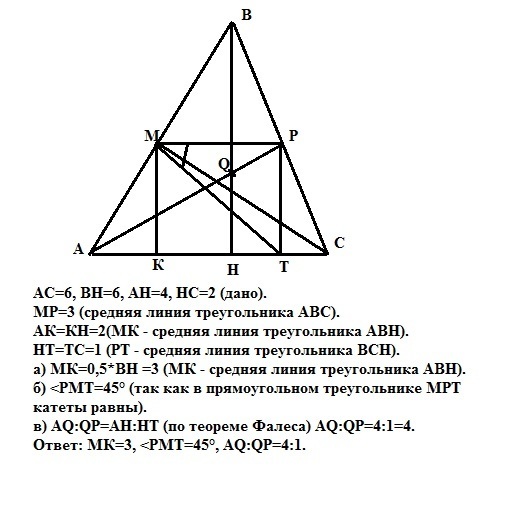
АС=6, ВН=6, АН=4, НС=2 (дано).
МР=3 (средняя линия треугольника АВС).
АК=КН=2(МК - средняя линия треугольника АВН).
НТ=ТС=1 (РТ - средняя линия треугольника ВСН).
а) МК=0,5*ВН =3 (МК - средняя линия треугольника АВН).
б) <PMT=45° (так как в прямоугольном треугольнике МРТ катеты равны).
в) AQ:QP=AH:HT (по теореме Фалеса) AQ:QP=4:1=4.
Ответ: МК=3, <PMT=45°, AQ:QP=4:1.