Предмет: Геометрия,
автор: Аноним
ДАЮ 20 БАЛЛОВ
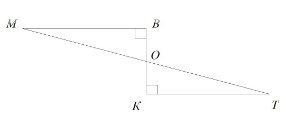
Прямая ВК перпендикулярна прямым МВ и КТ. Докажите, что треугольники МВО и ОКТ равны. Найдите углы ОМВ, ВОМ, ОТК, если известно, что МВ=КТ, а угол ТОК=40. (Обязательно доказательство равенства треугольников)
__________________________________________________________________
ЕСЛИ ХОТИТЕ ЛУЧШИЙ ОТВЕТ ТО НАДО НАПИСАТЬ
ДАНО:
И
РЕШЕНИЕ
Приложения:
Ответы
Автор ответа:
0
Дано:
треугольники OBM и TKO
угол B = 90°, угол K = 90°
MB = KT; угол TOK = 40°
Доказать: OBM = TKO
Найти: углы OMB, BOM, OTK
Решение/доказательство:
MB = KT (по условию), |
угол B = углу K (по условию) | => OBM = TKO (по двум сторонам и углу между ними)
BO = OK (точка О - центр) |
т.к угол TOK = 40°, угол K = 90°, то, по сумме угол треугольника угол OTK будет равен 180° - (40°+90°) = 50°
Углы OTK и OMB будут равны, т.к треугольники равны, => угол OMB = 50°
угол BOM соотвественно равен 40°
Ответ: 50°, 50°, 40°
треугольники OBM и TKO
угол B = 90°, угол K = 90°
MB = KT; угол TOK = 40°
Доказать: OBM = TKO
Найти: углы OMB, BOM, OTK
Решение/доказательство:
MB = KT (по условию), |
угол B = углу K (по условию) | => OBM = TKO (по двум сторонам и углу между ними)
BO = OK (точка О - центр) |
т.к угол TOK = 40°, угол K = 90°, то, по сумме угол треугольника угол OTK будет равен 180° - (40°+90°) = 50°
Углы OTK и OMB будут равны, т.к треугольники равны, => угол OMB = 50°
угол BOM соотвественно равен 40°
Ответ: 50°, 50°, 40°
Похожие вопросы
Предмет: Русский язык,
автор: bebebbenebebd
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: nikitasikorskji
Предмет: Химия,
автор: ilyin2014