Question

Составьте уравнение касательной к графику функции:
y=x²-3x+5 в точке с абсциссой x0=-1
Полный ответ

Answer 1

y=x²-3x+5   x₀=-1
f(-1)=(-1)²-3*(-1)+5
f(-1)=9
Производная:
f`(x₀)=Δ/(Δx(5))-3(Δ/Δx(x))+Δ/Δx(x²)=
f`(x₀)=-3(Δ/Δx(x)+Δ/Δx(x²)+0=
f`(x₀)=-3(Δ/Δx(x)+Δ/Δx(x²)=
f`(x₀)=Δ/Δx(x²)-1*3=
f`(x₀)=2x-3
f`(-1)=-5
Касательная:
y=f`(x₀)*(x-x₀)+f(x₀)
y=-5(x-(-1))+9
y=-5x+4
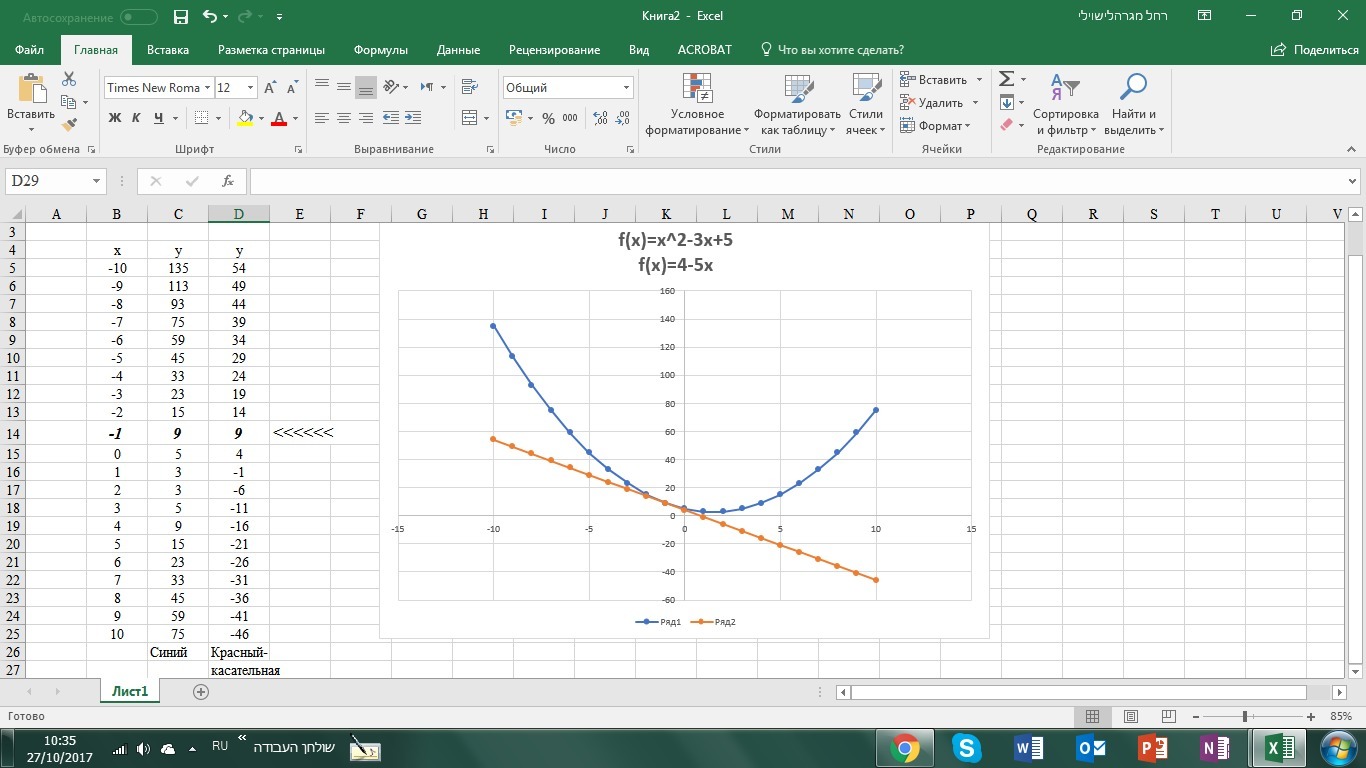
Ответ: уравнение касательной f(x)=x²-3x+5 в точке х₀=-1  имеет вид f(x)=-5x+4,
Точка касания (-1;9)
Прилагаю график для наглядности ( красным цветом выделена касательная)