Предмет: Алгебра,
автор: ArtSchoolMan
Помогите решить уравнение. Квадратные корни.
Приложения:
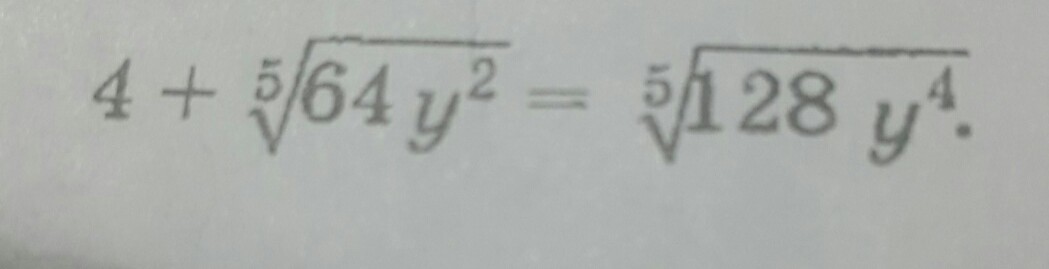
Ответы
Автор ответа:
0
Замена:
Обратная замена:
нет корней
Ответ:
Автор ответа:
0
Спасибо!
Похожие вопросы
Предмет: Литература,
автор: Ziktor
Предмет: Русский язык,
автор: galkalmoc111
Предмет: Русский язык,
автор: Texnof
Предмет: Биология,
автор: GusevVasily
Предмет: Алгебра,
автор: таня555372