Предмет: Алгебра,
автор: koly5075
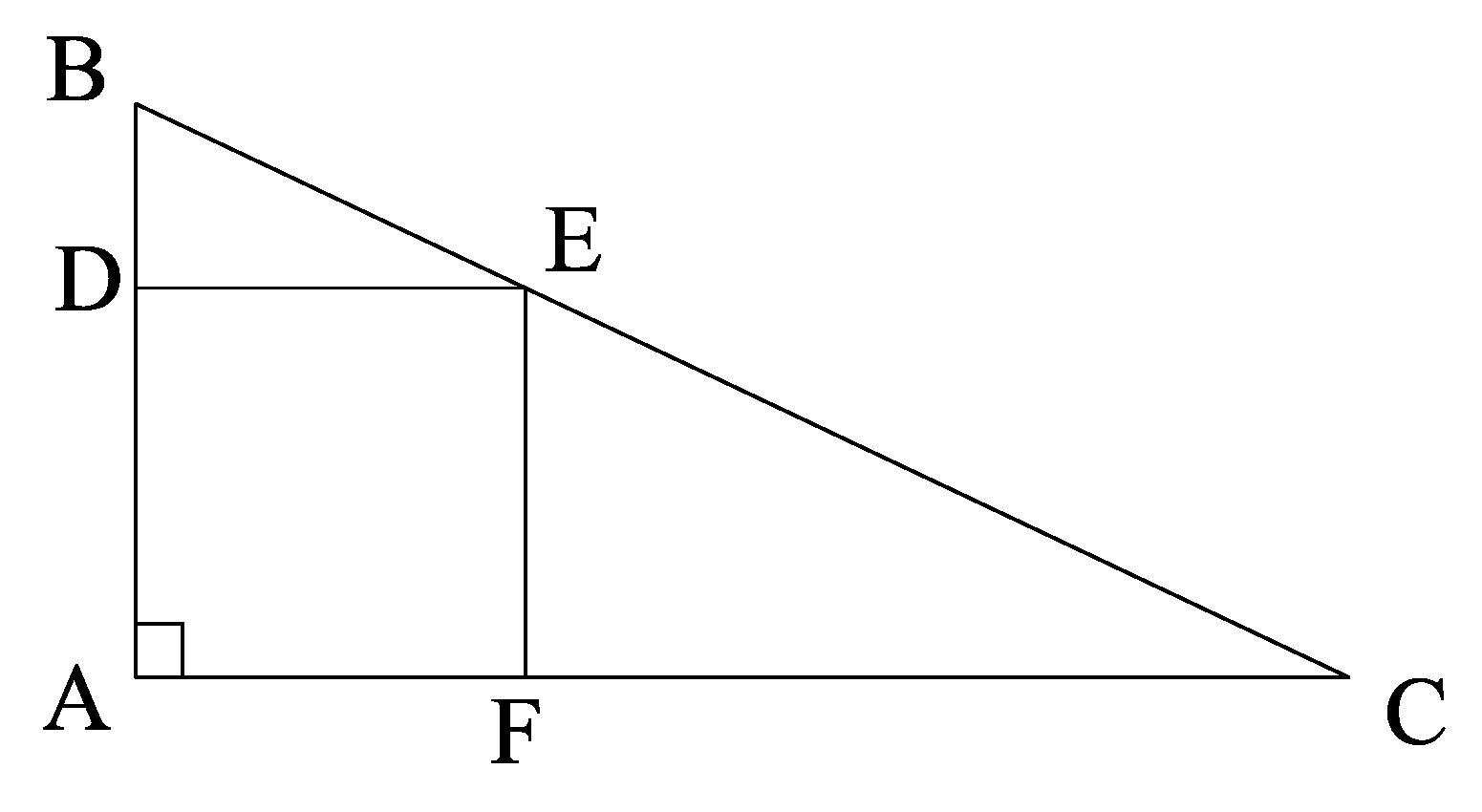
В прямоугольный треугольник ABC с прямым углом A и катетами AB=2, AC=6 вписан квадрат ADEF. Найдите отношение площади треугольника EFC к площади квадрата ADEF
Приложения:
Ответы
Автор ответа:
0
Задание № 6:
В прямоугольный треугольник ABC с прямым углом A и катетами AB=2, AC=6 вписан квадрат ADEF. Найдите отношение площади треугольника EFC к площади квадрата ADEF.
РЕШЕНИЕ: Пусть сторона квадрата х. Тогда FC=(6-x).
Площадь треугольника EFC=CF*FE/2=(6-x)x/2
Площадь квадрата равна х^2.
Их отношение: ((6-x)x/2)/х^2=(6-x)/2х.
Так как треугольники САВ и CFE подобны (по прямому углу и углу С), то составляем пропорцию:
АС/FC=AB/FE
6/(6-x)=2/x
6x=2(6-x)
6x=12-2x
8x=12
x=1.5
(6-x)/2х=(6-1.5)/(2*1.5)=1.5
ОТВЕТ: 1.5
Похожие вопросы
Предмет: Математика,
автор: kraubnervladimir
Предмет: Английский язык,
автор: vitusn13
Предмет: Алгебра,
автор: Аноним
Предмет: Биология,
автор: лол186
Предмет: Математика,
автор: vinogradova7