Question

решить номера 57, 59

Answer 1

№57
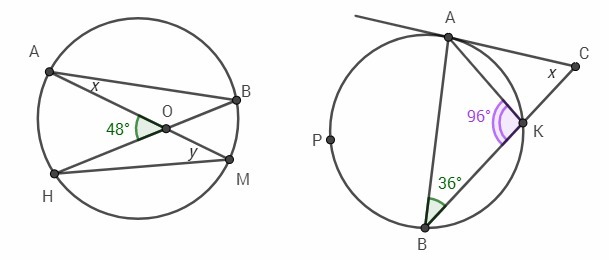
Вписанные углы, опирающиеся на одну и ту же дугу равны, отсюда:
∠МАВ = ∠МНВ = х  (оба опираются на дугу МВ)
∠АВН = ∠АМН = у  (оба опираются на дугу АН)

∠АОВ = 180° - ∠АОН = 180 - 48 = 132°  (смежные углы)

Сумма углов треугольника = 180°, в треугольнике АОВ ∠АОВ = 132°, следовательно, сумма двух других углов: 
х + у = 180 - 132 = 48°

Ответ: 48°
__________________________________________________________

№59

Вписанный угол равен половине дуги, на которую он опирается, отсюда:
Дуга АК = 2 * ∠АВК = 2 * 36 = 72°
Дуга АРВ = 2 * ∠АКВ = 2 * 96 = 192°

СВ - секущая, СА - касательная.
Угол между касательной и секущей равен полуразности высекаемых ими дуг, отсюда:
х = (192 - 72)/2 = 60°

Ответ: 60°