Question

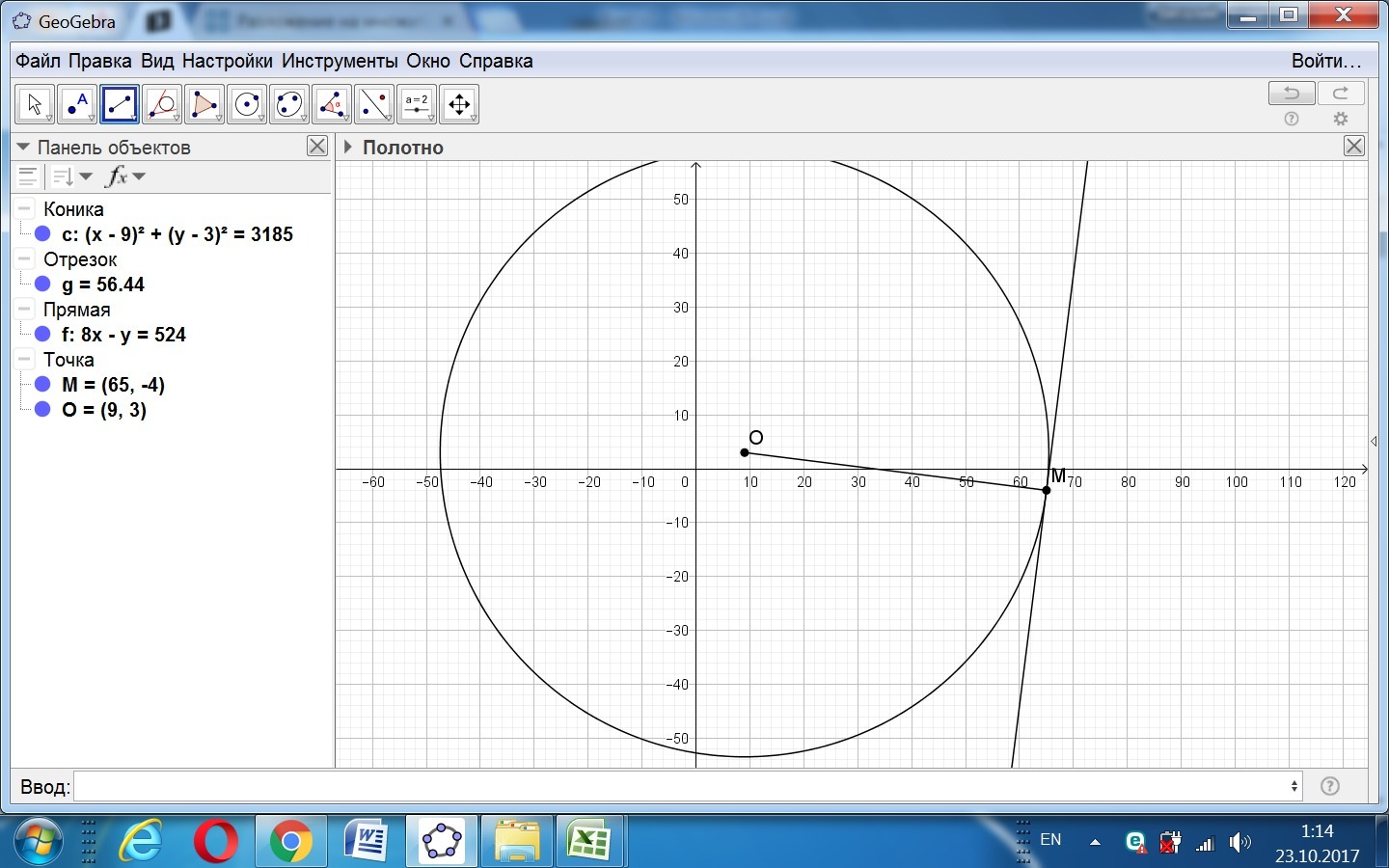
Запишите уравнение касательной к окружности(x−9)2+(y−3)2=3185 в точке M0(65,−4) в виде y=kx+d. В ответ введите через точку с запятой значения: k;d

Answer 1

Центр окружности - точка О(9; 3). Точка М(65; -4).
Уравнение ОМ: (х - 9)/(65-9) = (у - 3)/(-4-3),
                                (х - 9)/56 = (у + 3)/(-7).
В общем виде: -7х + 63 = 56у - 168,
                            7х + 56у - 231 = 0, сократим на 7:
                              х + 8у - 33 = 0.
В виде с коэффициентом: у = (-1/8)х + (33/8).
Касательная в точке М имеет к = -1/(-1/8) = 8.
Её уравнение у = 8х + в.
Найдём в, подставив координаты точки М:
-4 = 8*65 + в,
в = -4 - 520,
в = -524.
Ответ: уравнение касательной у = 8х - 524.

Answer 2

Благодарю за решение, а в ответ введите через точку с запятой значения: k;d- что необходимо подставить?

Answer 3

Это коэффициенты уравнения: 8 и -524.