Question

докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма

Answer 1

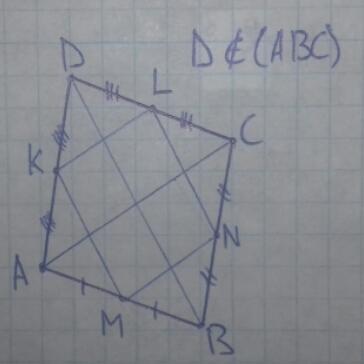
M, N, L и K середины сторон AB, BC, CD и DA соответственно.

Отрезок соединяющий середины двух сторон в треугольнике является средней линией, которая параллельна третьей стороне.

MN, NL, LK и KM среднии линии в ΔABC, ΔBCD, ΔCDA и ΔDAB соответственно. Значит MN║AC; NL║BD; LK║CA=AC; KM║DB=BD.

MN║AC║LK ⇒ MN║LK - по транзитивности параллельных прямых а пространстве.

Так же NL║KM (NL║BD║KM).

В четырёхугольнике MNLK противоположные стороны параллельны (MN║LK и NL║KM), то есть это параллелограмм. А точки M, N, L и K его вершины. Доказано.