Предмет: Алгебра,
автор: фекла5678
решите пожалуйста номер 29.25 под буквой б)
Приложения:
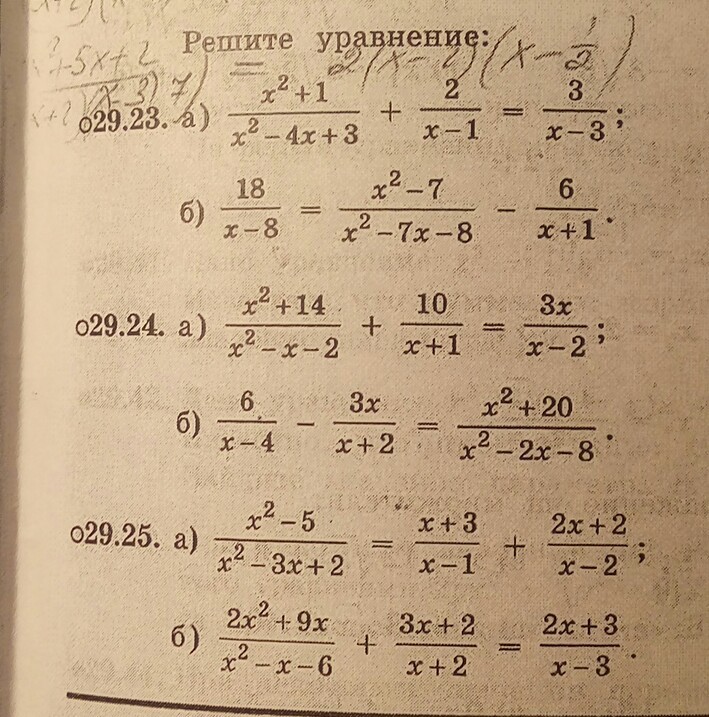
Ответы
Автор ответа:
0
Разложим знаменатель первой дроби на множители:
Перенесем дробь из правой части в левую:
Приведем все дроби к общему знаменателю и запишем числители над общим знаменателем:
Выполняем действия, раскрываем скобки:
Приводим подобные члены:
Разложим на множители числитель:
В любой дроби числитель может быть равен нулю, но знаменатель - никогда. То есть:
Тогда решаем уравнение:
Если произведение равно нулю, то один из множителей равен нулю. То есть либо:
либо:
Решаем:
Выражение верно, поэтому
Выражение верно, поэтому
Проверяем верно ли
1)
2)
Выражение верно, значит и значения
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: annamaya2015
Предмет: Английский язык,
автор: dianasajfullina22
Предмет: Математика,
автор: rahimzhan280783
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: Dog9991