Предмет: Алгебра,
автор: SAHARIA
Решите уравнение с помощью замены переменной
Приложения:
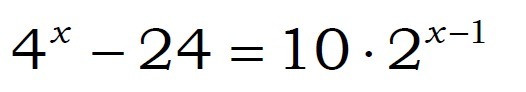
Ответы
Автор ответа:
0
2^x=a; a^2-24=10*1/2*a; a^2-5a-24=0; D=(-5)^2-4*1*(-24)=25+96=121; a1=(5-11)/2; a2=(5+11)/2; a1= -3; a2=8. 2^x= -3(корней нет), 2^x=8, 2^x=2^3, x=3. Ответ: x=3.
Автор ответа:
0
Автор ответа:
0
https://znanija.com/task/25930092
Похожие вопросы
Предмет: Математика,
автор: d11092011
Предмет: Математика,
автор: aizhandaniarova64
Предмет: Английский язык,
автор: dariashin
Предмет: Литература,
автор: Байышова
Предмет: История,
автор: KirilLL177030