Question

Прошу,молю, очень надо до завтрашнего утра решить задачу Г

Answer 1

Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

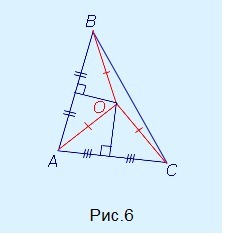
      Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам   AC   и   AB   треугольника   ABC,   и обозначим точку их пересечения буквой   O   (рис. 6).

Рис.6

      Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   AC,   то в силу теоремы 1 справедливо равенство:

CO = AO .

      Поскольку точка O лежит на серединном перпендикуляре к отрезку   AB,   то в силу теоремы 1 справедливо равенство:

AO = BO .

      Следовательно, справедливо равенство:

CO = BO ,

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку   BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

      Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

      Доказательство. Рассмотрим точку   O,   в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника   ABC   (рис. 6).

      При доказательстве теоремы 3 было получено равенство:

AO = OB = OC ,

из которого вытекает, что окружность с центром в точке   O   и радиусами   OA,   OB,   OC   проходит через все три вершины треугольника   ABC,   что и требовалось доказать.