Предмет: Алгебра,
автор: jeffthe
Решить уравнение с объяснением и ответом , пожалуйста
Приложения:
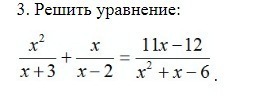
Ответы
Автор ответа:
1
Область допустимых значений:
Итак, x ≠ -3 и x ≠ 2
Левую часть приводим к общему знаменателю:
Знаменатели равны, значит равны и числители:
Уравнение кубическое, попробуем решить его разложением на множители. Известно, что корнями любого уравнения есть делители свободного члена (+12). Методом подбора выясняем, что x = 2 есть корень уравнения, значит:
Решением этого уравнения являются x = 2 и x = -3. Однако как раз эти значения не входят в область допустимых значений!
Ответ: уравнение решений не имеет.
Похожие вопросы
Предмет: Українська мова,
автор: artemvivdich3211
Предмет: Английский язык,
автор: 8v5fsqqsqf
Предмет: История,
автор: griskoa64
Предмет: Математика,
автор: mariabazelinska
Предмет: Химия,
автор: tovsikanna