Предмет: Геометрия,
автор: darytish
Народ помогите пожалуйста!!!! Очень нужно
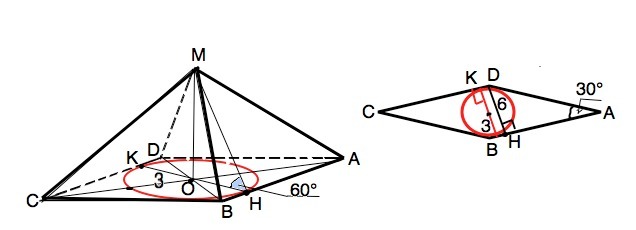
Основанием пирамиды является ромб, острый угол которого равен 30°. Все боковые грани пирамиды наклонены к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды, если радиус окружности, вписанной в ее основание, равен 3 списанной в ее основание, равен 3 см.
Ответы
Автор ответа:
3
Обозначим пирамиду MABCD, МО - высота пирамиды, МН - высота боковой грани.
Так как все грани наклонены к основанию под одинаковым углом, высоты граней равны между собой и их проекции равны радиусу вписанной в основание окружности.
МН=ОН:cos∠МНО=3•cos60°=6.
Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней или произведению высоты грани на полупериметр основания, что то же самое.
Рассмотрим основание ABCD пирамиды MABCD.
Диаметр вписанной в ромб окружности равен высоте этого ромба. Радиус вписанной окружности по условию равен 3.
d=КВ=2r=6
Высота DH=d=6
DH⊥АВ, противолежит углу 30°⇒сторона ромба АВ=2•DH=12
Периметр ромба 12•4=48.
Ѕ(бок)=МН•Р:2=6•48:2=144 (ед. площади)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: salkenovadilnaz
Предмет: Қазақ тiлi,
автор: mratsarapat8
Предмет: Английский язык,
автор: isaalbek11
Предмет: Английский язык,
автор: alina99855
Предмет: Обществознание,
автор: Galysha1965