Предмет: Геометрия,
автор: ужнеужели
Имеются ли закономерности расположения точек пересечения серединных перпендикуляров противолежащих сторон четырехугольника относительно середин его диагоналей, если его параллелограмм Вариньона имеет равные стороны (то есть диагонали четырехугольника равны)?
Ответы
Автор ответа:
0
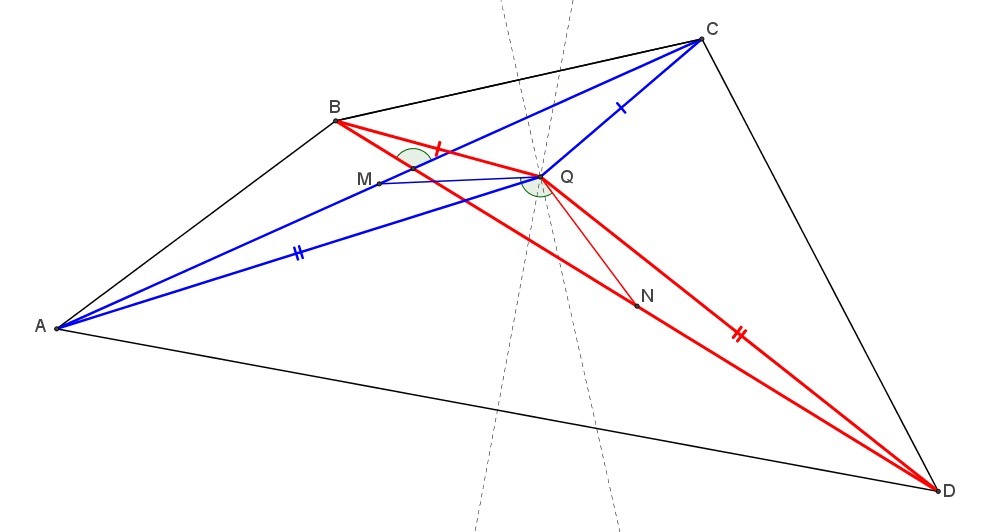
Имеются. Например, если в четырехугольнике ABCD диагонали равны, серединные перпендикуляры к отрезкам BC и AD пересекаются в точке Q, а М и N - середины диагоналей AC и BD соответственно, то QN=QM и ∠NQM равен углу между диагоналями четырехугольника.
Действительно, треугольники AQC и DQB очевидно равны по трем сторонам, а значит совмещаются поворотом вокруг точки Q (синий и красный треугольники). Значит их медианы QN и QM тоже совместятся при этом повороте, т.е. QN=QM и ∠MQN равен углу между прямыми AC и DB (т.к. диагональ AC переходит в DB).
Действительно, треугольники AQC и DQB очевидно равны по трем сторонам, а значит совмещаются поворотом вокруг точки Q (синий и красный треугольники). Значит их медианы QN и QM тоже совместятся при этом повороте, т.е. QN=QM и ∠MQN равен углу между прямыми AC и DB (т.к. диагональ AC переходит в DB).
Приложения:
Автор ответа:
0
Гениально
Автор ответа:
0
Мне кажется, отсюда должно получиться и решение задачи https://znanija.com/task/25852213. Раз угол MQN= углу BTC (T - пересечение диагоналей), то угол MPN (P - точка пересечения второй пары серединных перпендикуляров) будет равен углу ATB
Автор ответа:
0
Да, именно так.
Похожие вопросы
Предмет: Математика,
автор: safiya0abzhalimova
Предмет: Русский язык,
автор: milenazaika84
Предмет: Биология,
автор: shashelnikita
Предмет: Математика,
автор: хабиб14
Предмет: Математика,
автор: дима319