Предмет: Математика,
автор: kaads
Как это доказывается через индуктивный метод?
Приложения:
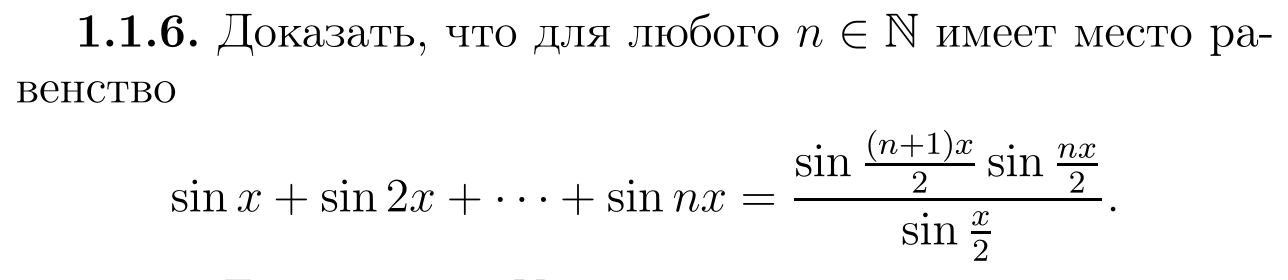
Ответы
Автор ответа:
0
База индукции
при n=1 тождество верно
Гипотеза индукции
Пусть тождество верно при натуральном n=k
Индукционный переход
Докажем что тогда тождество верно и при n=k+1
 используем гипотезу индукции
используем гипотезу индукции


использовали формулу синуса двойного угла и вынесли общий множитель за скобки

используем формулу умножения синуса на косинус

обычные преобразования дробей

используем нечетность синуса

получаем нужное равенство для n=k+1

По приниципу математической индукции тождество верно для любого натурального значения числа n
при n=1 тождество верно
Гипотеза индукции
Пусть тождество верно при натуральном n=k
Индукционный переход
Докажем что тогда тождество верно и при n=k+1
использовали формулу синуса двойного угла и вынесли общий множитель за скобки
используем формулу умножения синуса на косинус
обычные преобразования дробей
используем нечетность синуса
получаем нужное равенство для n=k+1
По приниципу математической индукции тождество верно для любого натурального значения числа n
Похожие вопросы
Предмет: Алгебра,
автор: kicherneva17
Предмет: Информатика,
автор: ytkaVtanke
Предмет: Английский язык,
автор: vladuxa5437
Предмет: Алгебра,
автор: rigge