Question

Сделайте рисунок
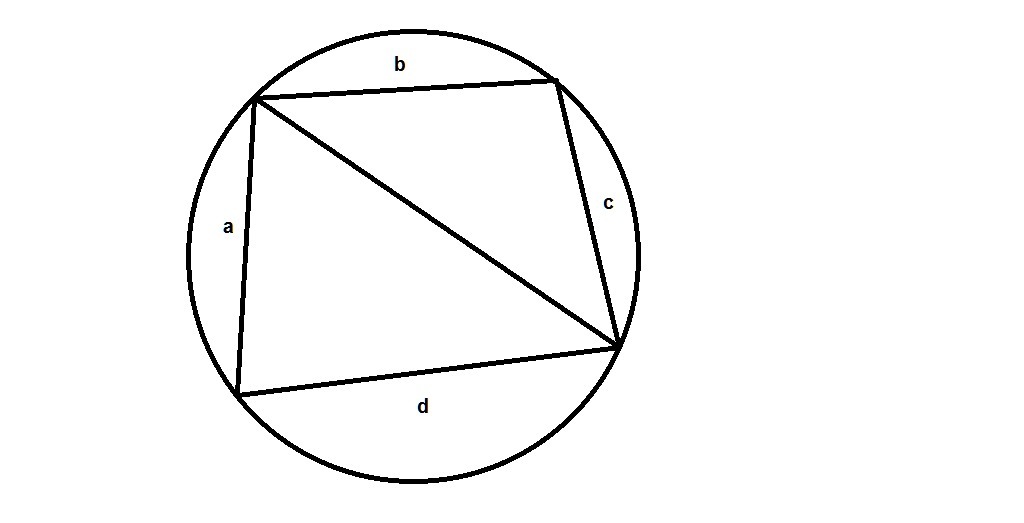
Стороны четырехугольника, взятые последовательно, равны a, b, c и d. Найдите косинус угла между сторонами b и c, если около четырехугольника можно описать окружность.

Answer 1

Сумма противоположных углов вписанного четырехугольника равна 180°.
α+β=180°
Отсюда следует, что косинусы этих углов противоположны
cosα=-cosβ

Проведем в четырехугольнике диагональ и выразим ее по теореме косинусов с двух сторон
$d_1^2=b^2+c^2-2bc*cos alpha \ d_1^2=a^2+d^2-2ad*cos beta$
приравниваем
$b^2+c^2-2bc*cos alpha =a^2+d^2-2ad*cos beta$
т.к. cosα=-cosβ
$b^2+c^2-2bc*cos alpha =a^2+d^2+2ad*cos alpha \ 2ad*cos alpha +2bc*cos alpha =b^2+c^2-a^2-d^2 \ cos alpha (2ad+2bc)=b^2+c^2-a^2-d^2 \ cos alpha = dfrac{b^2+c^2-a^2-d^2}{2ad+2bc}$

Answer 2

Спасибо огромное!)