Предмет: Математика,
автор: XoFF
Найти частное решение диф. уравнения, удовлетворяющее данным начальным условиям y"-6y'+25y=(32x-12)sin x - 36x cos 3x; y(0) = 4 ; y'(0) = 0
Приложения:
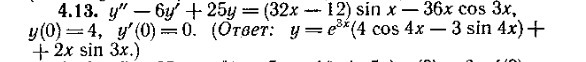
Ответы
Автор ответа:
0
Крч... либо условия косячные либо хз... но решение на ответ ни разу не походит:

Тут я тормозну... ибо я на бумаге я замучался их высчитывать... поэтому сразу пропишу готовые значения:


А теперь гвоздь программы: константы...

Тут я тормозну... ибо я на бумаге я замучался их высчитывать... поэтому сразу пропишу готовые значения:
А теперь гвоздь программы: константы...
Похожие вопросы
Предмет: Другие предметы,
автор: olakirsanova
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Snezha569
Предмет: Алгебра,
автор: artyomru1
Предмет: Математика,
автор: xvostatay