Предмет: Алгебра,
автор: мария1498
найдите площадь фигуры,ограниченной указанными линиями y=2x^2+1 и y=x^2+10
Ответы
Автор ответа:
0
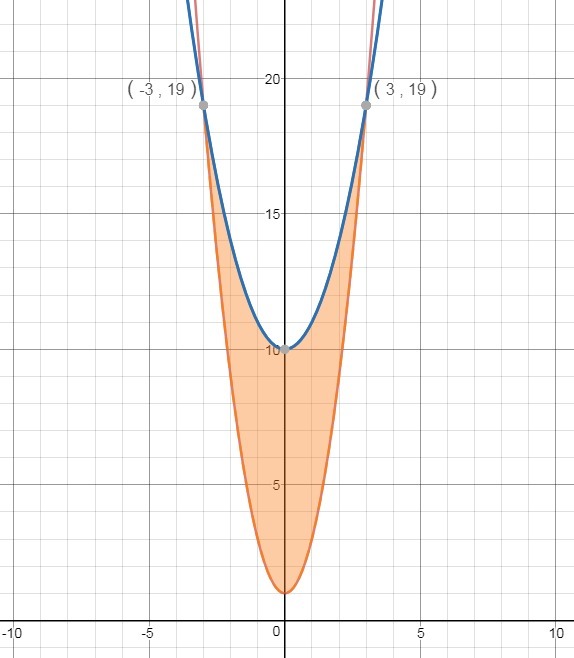
Для наглядности построим график функций и найдем точки их пересечения.

Чтобы найти площадь фигуры, ограниченной линиями, необходимо вычислить определенный интеграл.
Пределы интегрирования, мы уже нашли от -3 до +3.
Искомая площадь, как видно из графика, будет равна разности между площадями ограниченной графиком

и

Тогда


 кв.ед.
кв.ед.
Чтобы найти площадь фигуры, ограниченной линиями, необходимо вычислить определенный интеграл.
Пределы интегрирования, мы уже нашли от -3 до +3.
Искомая площадь, как видно из графика, будет равна разности между площадями ограниченной графиком
и
Тогда
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: ymonl7646
Предмет: Английский язык,
автор: maksatbakytzan02
Предмет: Математика,
автор: frazino666
Предмет: Математика,
автор: Abigael