Question

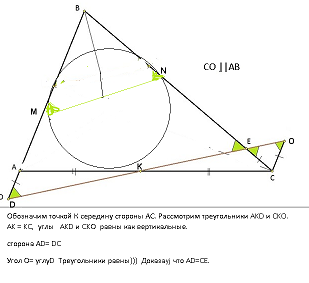
Окружность, вписанная в треугольник ABC, касается сторон AB и BC в точках M и N соответственно. Прямая, проходящая через середину стороны AC, параллельна MN и пересекает BA и BC в точках D и E соответственно. Доказать, что AD=CE.

Answer 1

см рисунок 
Обозначим точкой К середину стороны АС. Рассмотрим треугольники AKD и CKO. AK = KC,
углы   AKD и CKО  равны как вертикальные.CD|| AB 
в треугольнике ДСЕ угол ВЕД =углу ОЕС,как вертикальный, угол О=углу Д ( по построению) углы при основании равны значит тр-к ДСЕ равнобедренный
  Треугольники равны))) АД=СЕ