Question

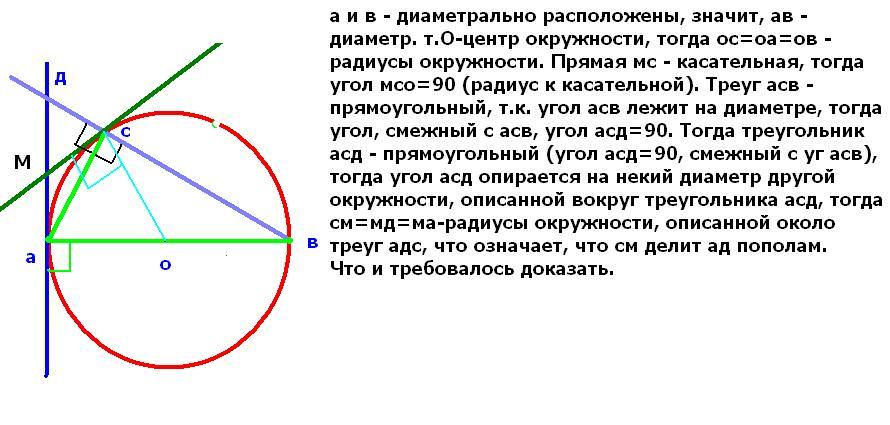
На окружности выбраны диаметрально противоположные точки A и B и отличная от них точка C. Касательная, проведённая к окружности в точке A, и прямая BC пересекаются в точке D. Доказать, что касательная, проведённая к окружности в точке C, делит пополам отрезок AD.

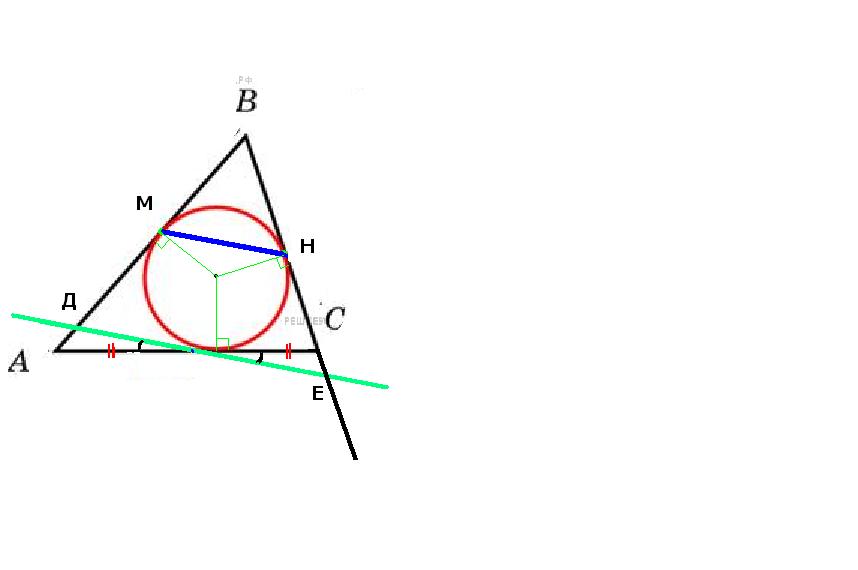
Окружность вписанная в треугольник ABC касается сторон AB и BC в точках M и N соответственно. Прямая проходит через середину AC параллельно прямой. МN пересекает прямые BA и BC в точках D и E соответственно. Доказать, что AD=CE.

Answer 1

Вложения...............................................