Question

ЧтороСтороны прямоугольника ab=9 bc=24. Точка m-середина стороны da. Отрезки ac и и mb пересекаются в точке k. Найдите bk.

Answer 1

Ответ:

BK = 10 (единиц)

Пошаговое объяснение:

Дано:

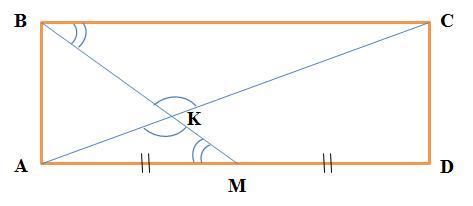
Прямоугольник ABCD (см. рисунок)

AB = CD = 9

BC = AD = 24

AM = MD

K - точка пересечения AC и MB  

Найти: BK

Решение.

1) Из AD = 24 и AM = MD имеем: AM = AD:2 = 24:2 = 12.

2) Так как ∠А = 90°, то треугольник ABM прямоугольный, поэтому верна теорема Пифагора:

BM² = AM² + AB² = 12² + 9² = 144 + 81 = 225 = 15²

или BM = 15.

3) ∠BKC = ∠AKM как вертикальные углы и ∠KBC = ∠KMA как накрест лежащие углы. Тогда по признаку подобия по двум углам

ΔBKC∼ΔAKM. В силу подобия

$displaystyle frac{BK}{MK} = frac{KC}{KA} =frac{BC}{AM}=frac{24}{12} =frac{2}{1}$

и BK = 2 · MK. Но BM = BK + KM = 2 · MK + MK = 3 · MK.

Отсюда

$displaystyle MK = frac{BM}{3}$ и

$displaystyle BK = frac{2*BM}{3} = frac{2*15}{3} = 10$

Что требовалось найти!