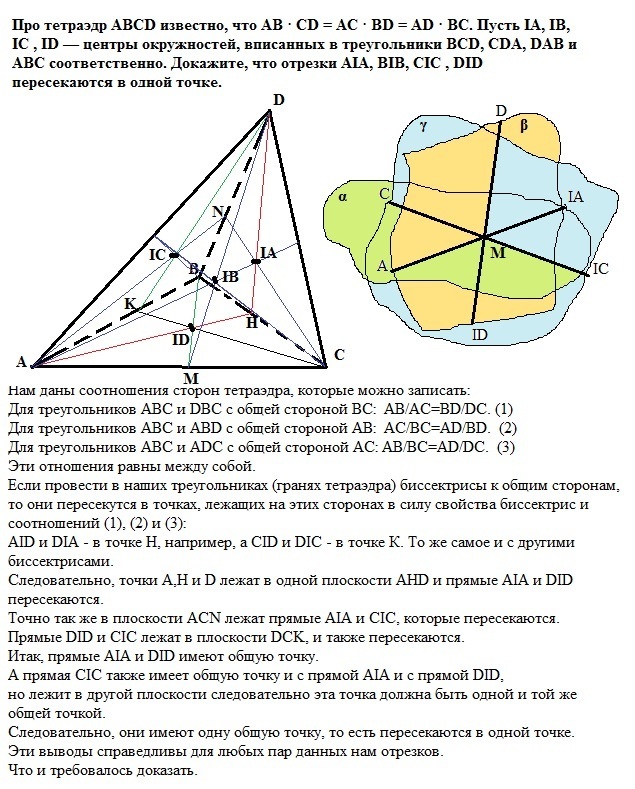
Про тетраэдр ABCD известно, что AB · CD = AC · BD = AD · BC. Пусть IA, IB, IC , ID — центры окружностей, вписанных в треугольники BCD, CDA, DAB и ABC соответственно. Докажите, что отрезки AIA, BIB, CIC , DID пересекаются в одной точке.
Ответы
Нам даны соотношения сторон тетраэдра:
AB*CD = AC*BD = AD*BC. Или, сгруппировав их по другому, имеем:
Для треугольников АВС и DBC с общей стороной ВС:
AB/AC=BD/DC. (1)
Для треугольников АВС и ABD с общей стороной АВ:
AC/BC=AD/BD. (2)
Для треугольников АВС и ADC с общей стороной АС:
AB/BC=AD/DC. (3)
Эти отношения равны между собой (дано).
Центр вписанной окружности треугольника лежит на пересечении биссектрис его внутренних углов, а биссектрисы делят противоположные стороны в отношении прилегающих сторон (свойство).
Причем это свойство имеет обратную силу, то есть, если прямая, проведенная из вершины угла треугольника делит противоположную сторону в отношении прилегающих сторон, то эта прямая - биссектриса
угла.
Если провести в наших треугольниках биссектрисы к общим сторонам, то
они пересекутся в точках, лежащих на этих сторонах в силу соотношений
(1), (2) и (3):
AID и DIA - в точке Н, например, а CID и DIC - в точке К. То же самое
и с другими биссектрисами.
Следовательно, точки А,Н и D лежат в одной плоскости АНD и прямые AIA и DID пересекаются.
Точно так же в плоскости АСN лежат прямые AIA и CIC, которые пересекаются.
Прямые DID и CIC лежат в плоскости DCK, и также пересекаются.
Итак, прямые AIA и DID имеют общую точку.
А прямая CIC также имеет общую точку и с прямой AIA и с прямой DID,
но лежит в другой плоскости, следовательно эта точка должна быть одной и той же общей точкой.
То же и с пересекающимися прямыми DID и ВIВ, которые лежат в
плоскости BMD.
Имеем четыре пары пересекающихся прямых (AIA и DID, AIA и CIC,
DID и CIC, DID и ВIВ), лежащих в четырех разных плоскостях (АНD,АСN,DCK и BMD соответственно).
Эти выводы справедливы для любых пар данных нам отрезков:
Если три или более прямых,лежащих в разных плоскостях, попарно
пересекаются, то они имеют одну общую точку.
Следовательно, данные нам отрезки пересекаются в одной точке.
Что и требовалось доказать.