Предмет: Геометрия,
автор: dodiddone
Решите пожалуйста задачу по геометрии 8 класс:
Дано: ABCD - параллелограмм,
АК биссектриса угла А,
BМ биссектриса угла B
Доказать: треугольник BOA - прямоугольный.
Приложения:
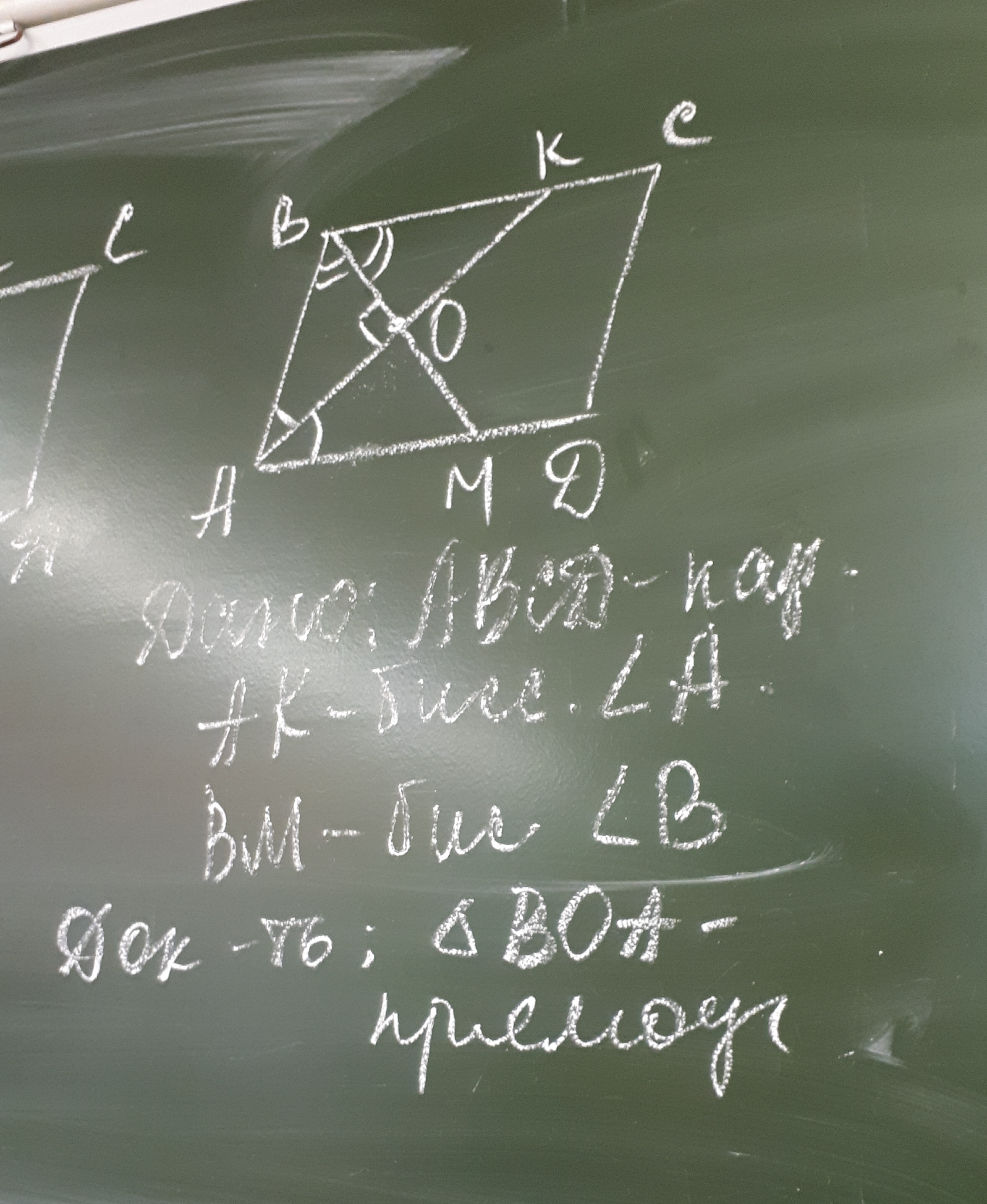
Ответы
Автор ответа:
0
В параллелограмме углы, прилежащие к одной стороне, равны в сумме 180°. <A+<B=180°. Значит <A/2+<B/2=(1/2)*(<A+<B)=90°.
В треугольнике ВОА сумма двух углов = 90°, значит третий угол =90° (так как сумма внутренних углов треугольника =180°).
Треугольник ВОА прямоугольный, что и требовалось доказать.
В треугольнике ВОА сумма двух углов = 90°, значит третий угол =90° (так как сумма внутренних углов треугольника =180°).
Треугольник ВОА прямоугольный, что и требовалось доказать.
Похожие вопросы
Предмет: Русский язык,
автор: saramelikova082
Предмет: Математика,
автор: laskotatana862
Предмет: Математика,
автор: Sonya105081
Предмет: Алгебра,
автор: lerabarbina199
Предмет: Алгебра,
автор: Adeliya123456789