Предмет: Алгебра,
автор: rahatik05
lim x^3-3x-2/x^3-8 x->2
Ответы
Автор ответа:
0
Приложения:
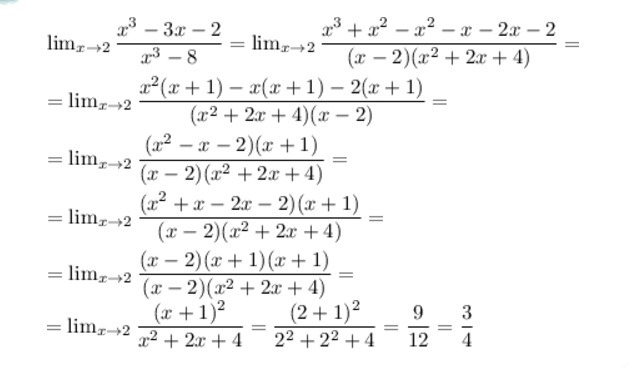
Автор ответа:
0
я хз что ты написал но спс
Автор ответа:
0
обнови страницу, я скрин добавил
Автор ответа:
0
а если один х из х^3 на 2 поменять?
Похожие вопросы
Предмет: История,
автор: isenovdaniar254
Предмет: Физика,
автор: usupovamihriban79
Предмет: Алгебра,
автор: gudkovakristina575
Предмет: Математика,
автор: yukalazas
Предмет: Алгебра,
автор: НаСтЕнОчКа8ПрОсТо