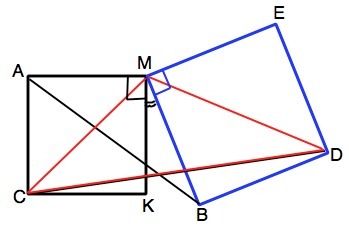
Двa квaдрaтa имеют oбщую вepшину . Нaйдитe oтнoшение отрезков AB и CD.
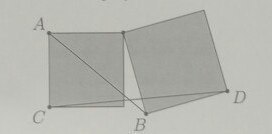
Ответы
Подробно:
Обозначим общую вершину квадратов М, а квадраты – САМК и ВМЕD. Проведем диагонали СМ и MD. Примем сторону АМ=m, сторону МЕ=b. Диагонали квадрата делят его углы на два по 45° => Из формулы диагонали квадрата d=a√2 следует СМ =m√2, MD =b√2.
Рассмотрим ∆ СМD и ∆ AМB ∠АМВ= ∠АМК+угол КМВ=90°+ угол КМВ. Угол СМD=СМК+ВМD+КМВ=2•45°+КМВ=90°+ КМВ. => ∠АМВ=∠СМD.
АМ:МВ=СМ:МD или а:b=a√2:b√2 Стороны ∆ АМВ и ∆ СМD пропорциональны.
«Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны» => ∆ АMВ~∆ CMD. Из подобия следует отношение АМ:СМ=АВ:СD. АМ:СМ – отношение стороны квадрата к его диагонали и равно m:m√2, т.е. 1/√2, что равно синусу 45°=√2/2 Это ответ.