Предмет: Математика,
автор: Inga30
Найдите пределы функции. Не пользуясь правилом Лопиталя.
Приложения:
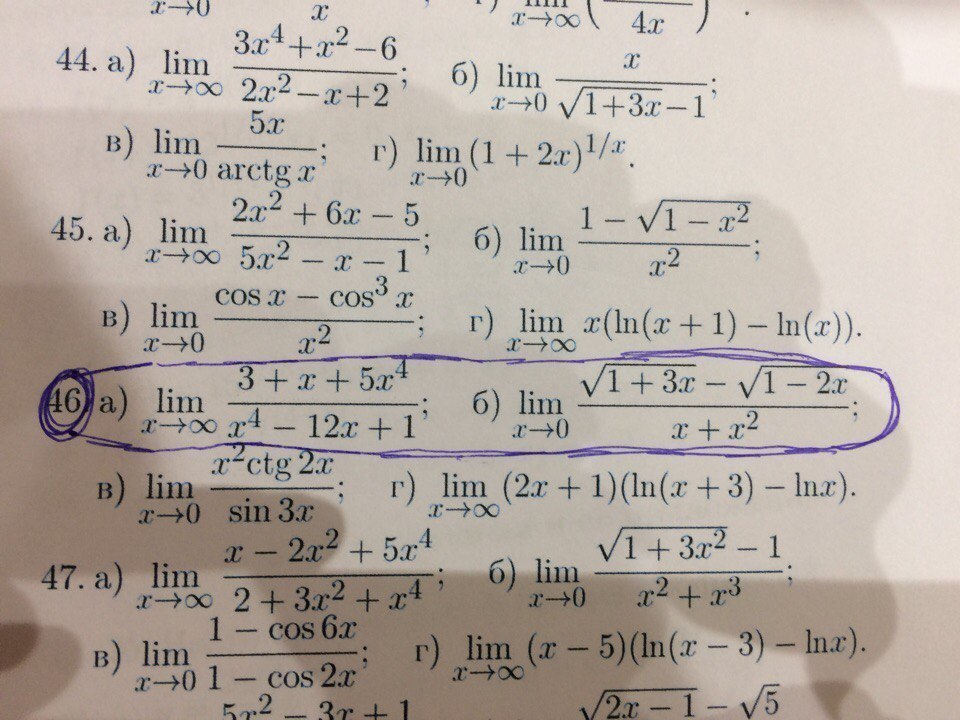
Ответы
Автор ответа:
0
46a) Неопределённость ∞/∞ раскрываем делением числителя и знаменателя на икс в максимальной степени, т.е. на 

46б) Неопределённость 0/0 раскрываем умножением числителя и знаменателя на выражение, сопряжённое числителю, т.е. на


46б) Неопределённость 0/0 раскрываем умножением числителя и знаменателя на выражение, сопряжённое числителю, т.е. на
Автор ответа:
0
-12/оо^2 + 1/oo^4. А попробуйте обновить страницу. Бывает не сразу формулы показываеются нормально.
Автор ответа:
0
это нули? верно?
Автор ответа:
0
Нет, это бесконечность. Вместо икса подставляется бесконечность - оо.
Автор ответа:
0
поняла, спасибо
Автор ответа:
0
посмотрите пожалуйста у меня еще задания от сегодняшнего числа, буду очень благодарна.
Похожие вопросы
Предмет: Информатика,
автор: nikzero1
Предмет: Английский язык,
автор: dakotablackcat66654
Предмет: Русский язык,
автор: julianapokrovska
Предмет: Математика,
автор: floflo0809
Предмет: Химия,
автор: klimenkol21