Question

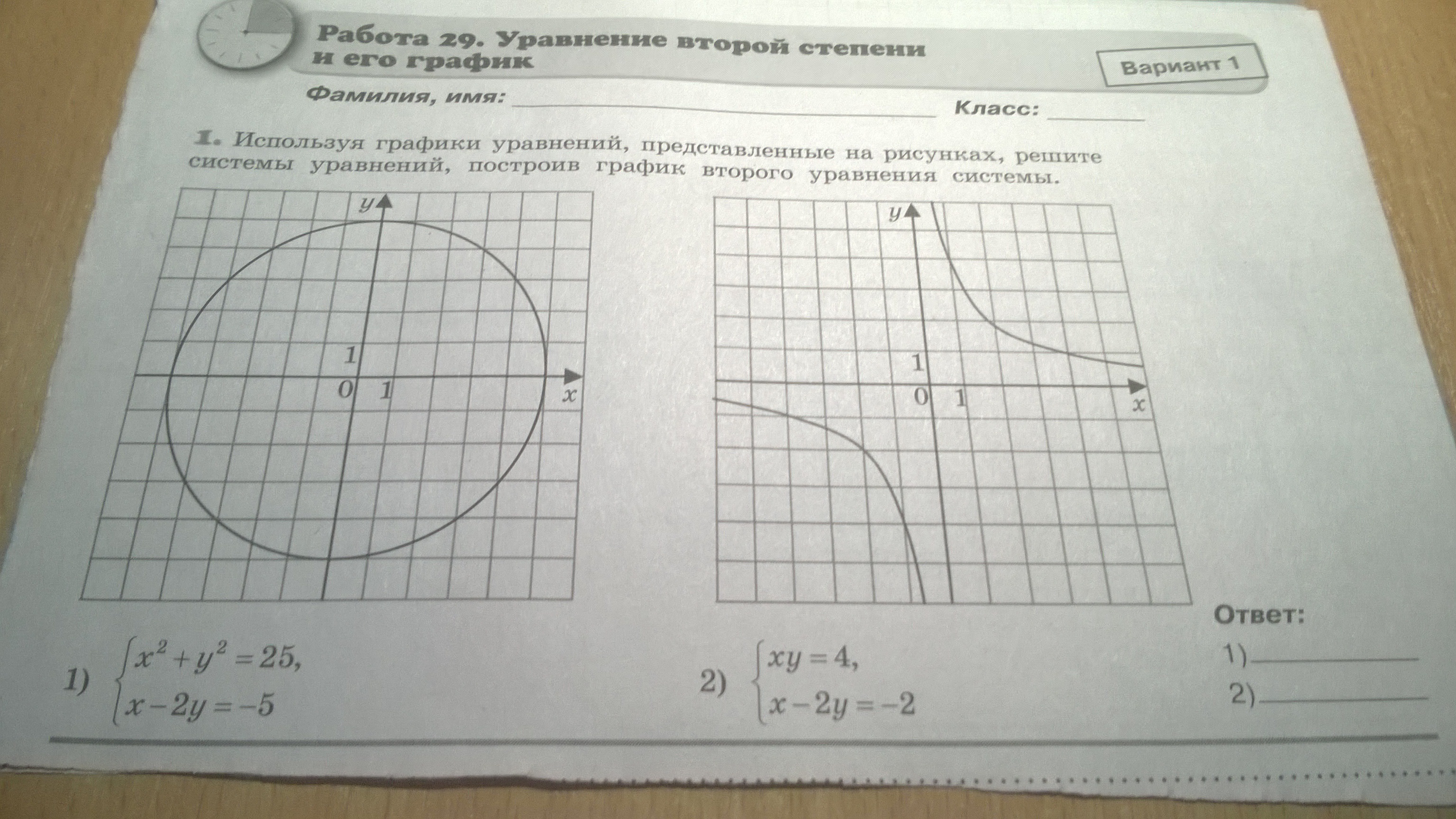
Напишите подробное решение двух систем.

Answer 1

Первая система:
x² + y² = 25
x - 2y = -5
Из второго уравнения выражаем х и подставляем в первое уравнение:
x = -5 + 2y
(-5 + 2y)² + y² = 25
25 - 20y + 4y² + y² = 25
25 - 20y + 5y² = 25
5y² - 20y + 25 = 25
5y² - 20y + 25 - 25 = 0
5y² - 20y = 0
5y (y - 4) = 0
y = 0; y = 4
Подставляем значения y в любое уравнение и находим значение х
y = 0
x² + 0² = 25
x = 5, x = -5

y = 4
x² + 4² = 25
x = 3; x = -3
Ответ: (0; 5); (0; -5); (4; 3); (4; -3)

Вторая система:
xy = 4
x - 2y = -2
Выражаем x из второго уравнения и подставляем в первое уравнение
x = -2 + 2y
(-2 + 2y)y = 4
-2y + 2y² = 4
2y² - 2y - 4 = 0
y² - y - 2 = 0
D = 1 - 4 • (-2) = 9
x1 = 1 - 3 / 2 = -1
x2 = 1 + 3 / 2 = 2
Подставляем значения х в любое уравнение и считаем значение y:
x = -1
xy = 4
-1y = 4
y = -4

x = 2
xy = 4
2y = 4
y = 2
Ответ: (-1; -4); (2; 2)