Предмет: Геометрия,
автор: Аlisa555
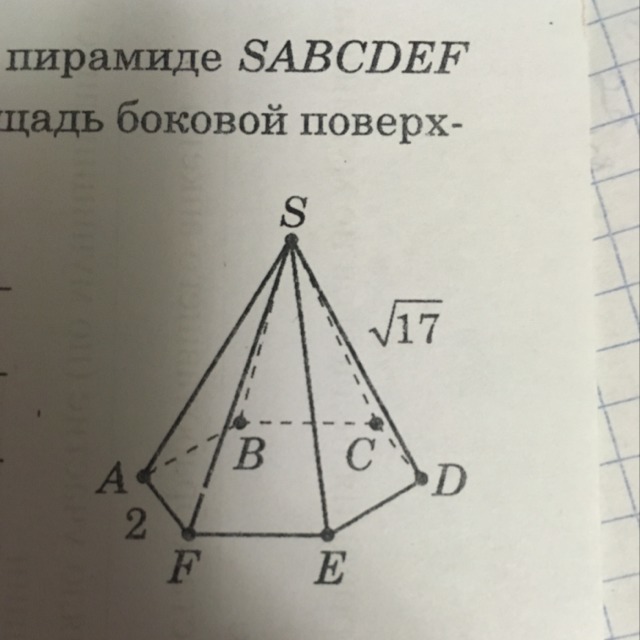
В правильной шестиугольной пирамиде SABCDEF AF=2, SD=√17. Найдите площадь боковой поверхности пирамиды.
Приложения:
Ответы
Автор ответа:
0
Как я уже говорил, радиус описанной окружности равен стороне
Пусть SO-высота пирамиды, тогда по теореме Пифагора высота равна
SO= . А зачем нам она не понятно, поэтому ищем площадь боковой поверхности
. А зачем нам она не понятно, поэтому ищем площадь боковой поверхности
S=6S1
S1=1/2AF*SH SH-высота в равнобедренном треугольнике
SH=4 (по теореме Пифагора)
S1=1/2*2*4=4
S=4*6=24
Пусть SO-высота пирамиды, тогда по теореме Пифагора высота равна
SO=
S=6S1
S1=1/2AF*SH SH-высота в равнобедренном треугольнике
SH=4 (по теореме Пифагора)
S1=1/2*2*4=4
S=4*6=24
Похожие вопросы
Предмет: Алгебра,
автор: nazarkkin2
Предмет: Физика,
автор: SaSmLo
Предмет: Геометрия,
автор: sofifox71
Предмет: Математика,
автор: Flatershai1