Question

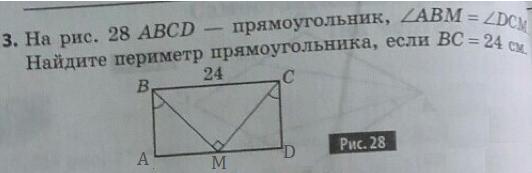
3.На рис.28 ABCD-прямоугольник, угол ABM=углу DCM. Найдите периметр прямоугольника, если BC=24 см

Answer 1

В прямоугольники углы при вершинах равны 90°, а противоположные стороны равна (AD=BC=24см)

ΔBAM = ΔCDM по катету и острому углу (∠ABM=∠DCM по условию;  BA=CD как противоположные стороны прямоугольника), поэтому BM=MC и AM=MD.

ΔBMC - прямоугольный (∠BMC=90°) и равнобедренный (BM=MC), поэтому ∠CBM=∠BCM =90°:2=45°.

∠DCM+∠BCM = ∠DCB = 90° как угол прямоугольника.

∠DCM = 90°-∠BCM = 90°-45° = 45°.

ΔCDM - равнобедренный т.к. это прямоугольный треугольник с острым углов в 45° (∠DCM=45°), поэтому CD=MD=AD:2=24см:2 = 12см.

CD=BA=12см.

$displaystyle P_{ABCD}$ = 2·(AB+BC) = 2·(12см+24см) = 2·36см = 72см.

Ответ: 72см.