Предмет: Алгебра,
автор: Mankeysy
Решите пожалуйста выражения
Приложения:
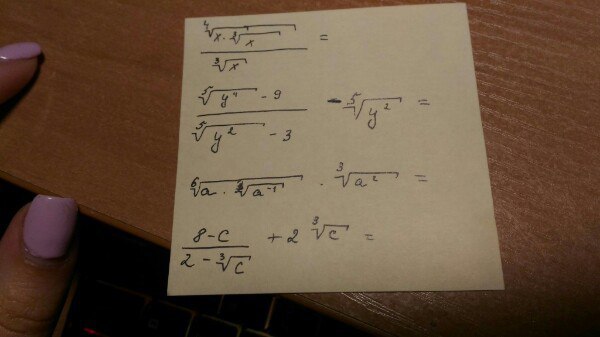
Ответы
Автор ответа:
0
1. (x * x^(1/3))^(1/4) / x^(1/3) = (x^(4/3))^(1/4) / x^(1/3) = x^(1/3) / x^(1/3) = 1, x <> 0
2. ( (y^4)^(1/5) - 9 )/( (y^2)^(1/5) - 3) - (y^2)^(1/5) = ( (y^(2/5))^2 - 9 )/( y^(2/5) - 3) - y^(2/5) = (y^(2/5) + 3)(y^(2/5) - 3)/(y^(2/5) - 3) - y^(2/5) = y^(2/5) + 3 - y^(2/5) = 3, y <> 3^(5/2)
3. (a * (a^(-1))^(1/3))^(1/6) * (a^2)^(1/3) = (a * a^(-1/3))^(1/6) * a^(2/3) = (a^(2/3))^(1/6) * a^(2/3) = a^(2/18 + 2/3) = a^(7/9), a <> 0
4. (8 - c)/(2-c^(1/3)) + 2c^(1/3) = (2 - c^(1/3))(4 + 2c^(1/3) + c^(2/3))/(2-c^(1/3)) + 2c^(1/3) = 4 + 2c^(1/3) + c^(2/3) + 2c^(1/3) = c^(2/3) + 4c^(1/3) + 2^2 = (c^(1/3) + 2)^2, c <> 8
2. ( (y^4)^(1/5) - 9 )/( (y^2)^(1/5) - 3) - (y^2)^(1/5) = ( (y^(2/5))^2 - 9 )/( y^(2/5) - 3) - y^(2/5) = (y^(2/5) + 3)(y^(2/5) - 3)/(y^(2/5) - 3) - y^(2/5) = y^(2/5) + 3 - y^(2/5) = 3, y <> 3^(5/2)
3. (a * (a^(-1))^(1/3))^(1/6) * (a^2)^(1/3) = (a * a^(-1/3))^(1/6) * a^(2/3) = (a^(2/3))^(1/6) * a^(2/3) = a^(2/18 + 2/3) = a^(7/9), a <> 0
4. (8 - c)/(2-c^(1/3)) + 2c^(1/3) = (2 - c^(1/3))(4 + 2c^(1/3) + c^(2/3))/(2-c^(1/3)) + 2c^(1/3) = 4 + 2c^(1/3) + c^(2/3) + 2c^(1/3) = c^(2/3) + 4c^(1/3) + 2^2 = (c^(1/3) + 2)^2, c <> 8
Похожие вопросы
Предмет: Алгебра,
автор: vtor69938
Предмет: Математика,
автор: ILia0102
Предмет: Математика,
автор: s83000
Предмет: Математика,
автор: Ulyana11205