Предмет: Алгебра,
автор: nastenka332
найдите все пары (х,у) чисел х и у , для которых( пример во вложении) . Помогите пожалуйста понять , как. такого типа примеры решаются; баллами не обижу
Приложения:
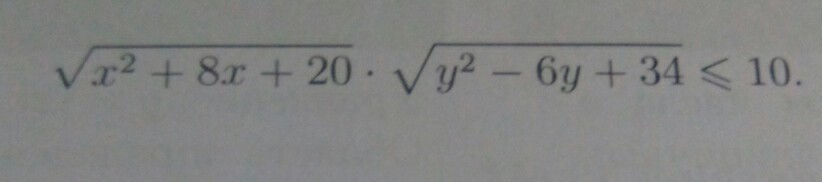
Ответы
Автор ответа:
0
task/25754256
--------------------
√(x²+8x +20)*√(y² -6y+34) ≤ 10
√((x+4)² +4) *√((y -3)²+25) ≥ √4*√25 =10
возможно , если √((x+4)² +4) *√((y -3)²+25) =10
т.е. если
{x+4 =0 { x =- 4
{y -3 =0 { y = 3
ответ : (-4 ; 3) .
--------------------
√(x²+8x +20)*√(y² -6y+34) ≤ 10
√((x+4)² +4) *√((y -3)²+25) ≥ √4*√25 =10
возможно , если √((x+4)² +4) *√((y -3)²+25) =10
т.е. если
{x+4 =0 { x =- 4
{y -3 =0 { y = 3
ответ : (-4 ; 3) .
Автор ответа:
0
спасибо большое за решение, но вы можете объяснить, почему мы х+4 и у-3 приравниваем нулю?
Автор ответа:
0
Получаются минимальные значения a) x²+8x +20 =x² +2x*4 +4² - 4² +20 = (x +4)² + 4 ≥ 4 т.к.(x +4)² ≥ 0 * * * min(x²+8x +20) =4 * * * b) y² -6y+34=y² -2y*3 +3² -3²+34 =(y -3)² +25 ≥ 25
Автор ответа:
0
спасибо большое)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: Аноним
Предмет: Алгебра,
автор: balashovamargaryta
Предмет: Литература,
автор: AndreykaNya
Предмет: Биология,
автор: Rina12495