Предмет: Алгебра,
автор: maniashik
Без понятия как решать. Ответ должен получиться 1/4 ; 2
Приложения:
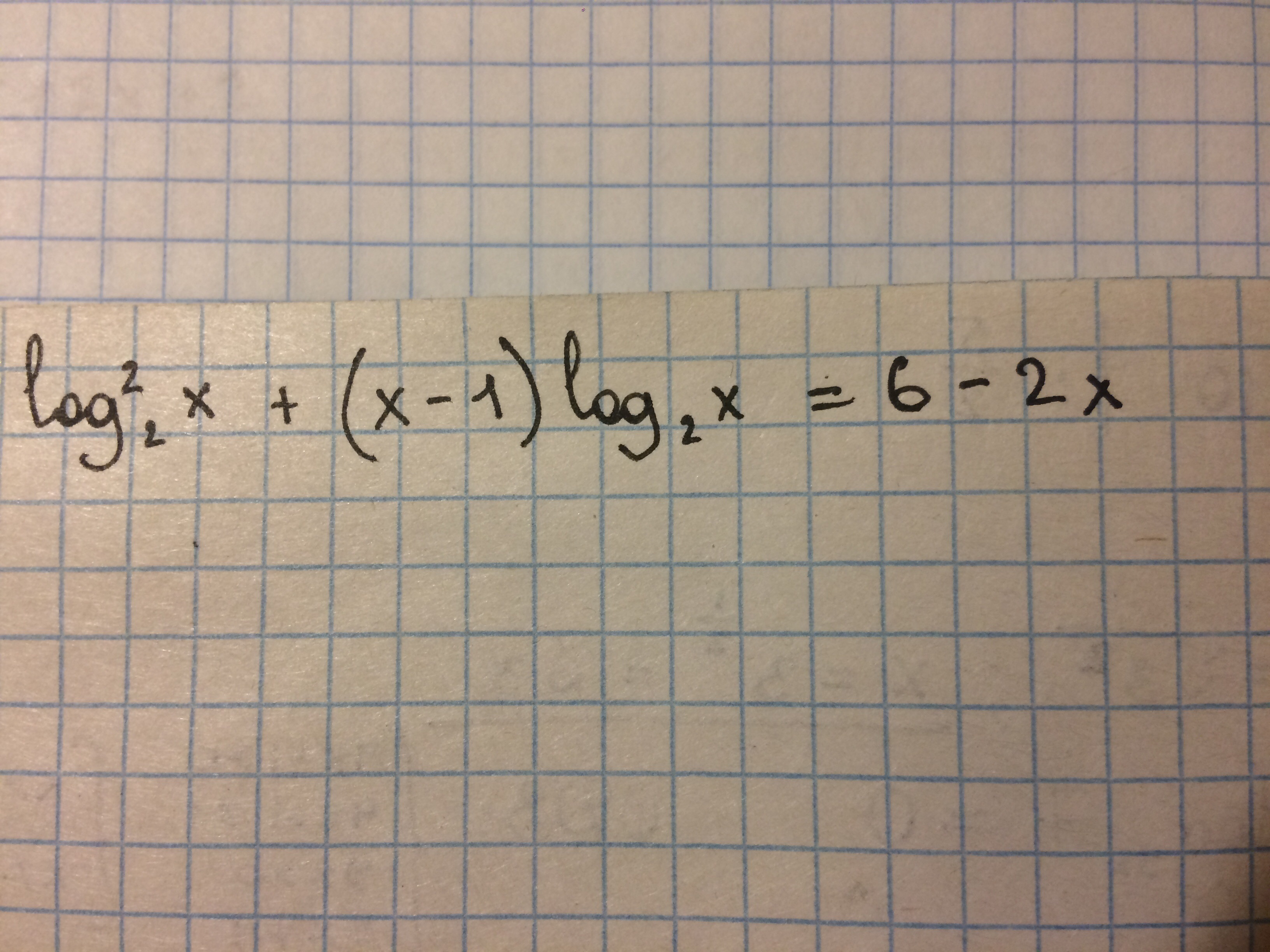
Ответы
Автор ответа:
0
одз:

решаем:

разложим на множители:
на множители:

тогда получим:

теперь осталось решить это уравнение:

мы знаем, что x>0, тогда из целых значений x нам подойдут x=1;2;3
проверяем:

значит
больше корней это уравнение не имеет
Ответ: 1/4; 2
решаем:
разложим
тогда получим:
теперь осталось решить это уравнение:
мы знаем, что x>0, тогда из целых значений x нам подойдут x=1;2;3
проверяем:
значит
больше корней это уравнение не имеет
Ответ: 1/4; 2
Похожие вопросы
Предмет: Информатика,
автор: luarmyl
Предмет: История,
автор: gjb26
Предмет: Беларуская мова,
автор: cofbaud19
Предмет: Математика,
автор: ariadnamilk03
Предмет: Математика,
автор: magataygibovvvv