Предмет: Геометрия,
автор: pro100vannuha
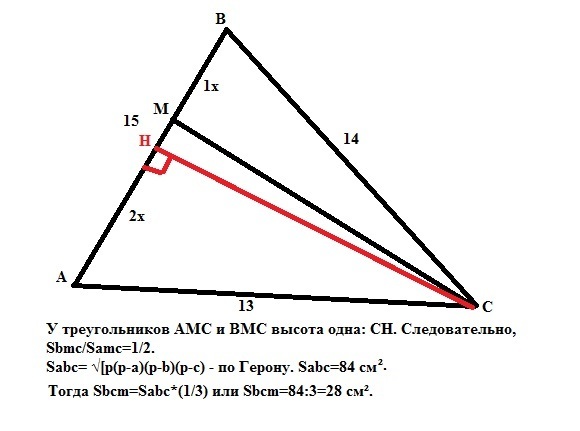
В треугольнике АВС известны длины сторон АВ = 15 см, ВС = 14 см, АС = 13 см.
точка М делит сторону АВ в отношении АМ : МВ = 2 : 1. Найдите площадь треугольника ВСМ.
Ответы
Автор ответа:
0
Повторяю решение:
Треугольники АСМ и ВСМ - треугольники с одной высотой, проведенной из вершины С к стороне АВ. Следовательно, их площади относятся как основания, к которому проведена высота, то есть Sbcm/Sacm=1/2.
Сумма этих площадей - площадь треугольника АВС, которую найдем ао Герону: Sabc=√[p(p-a)(p-b)(p-c)], где р - полупериметр. p=(13+14+15):2=21.
Sabc=√(21*6*7*8)=84 см².
Тогда Sbcm=Sabc*(1/3) или Sbcm=84:3=28 см².
Треугольники АСМ и ВСМ - треугольники с одной высотой, проведенной из вершины С к стороне АВ. Следовательно, их площади относятся как основания, к которому проведена высота, то есть Sbcm/Sacm=1/2.
Сумма этих площадей - площадь треугольника АВС, которую найдем ао Герону: Sabc=√[p(p-a)(p-b)(p-c)], где р - полупериметр. p=(13+14+15):2=21.
Sabc=√(21*6*7*8)=84 см².
Тогда Sbcm=Sabc*(1/3) или Sbcm=84:3=28 см².
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: vahromkinaoksana
Предмет: Геометрия,
автор: firemari25
Предмет: Геометрия,
автор: trippf1ll
Предмет: Право,
автор: ктотоэтоя
Предмет: Алгебра,
автор: настяополрп