Question

Диагональ прямоугольника, вписанного в окружность, равна 10см, а его площадь 48см  квадратных. Найдите радиус описанной окружности и стороны прямоугольника. 
Пожалуйста помогите решение нужно полностью и сейчас

Answer 1

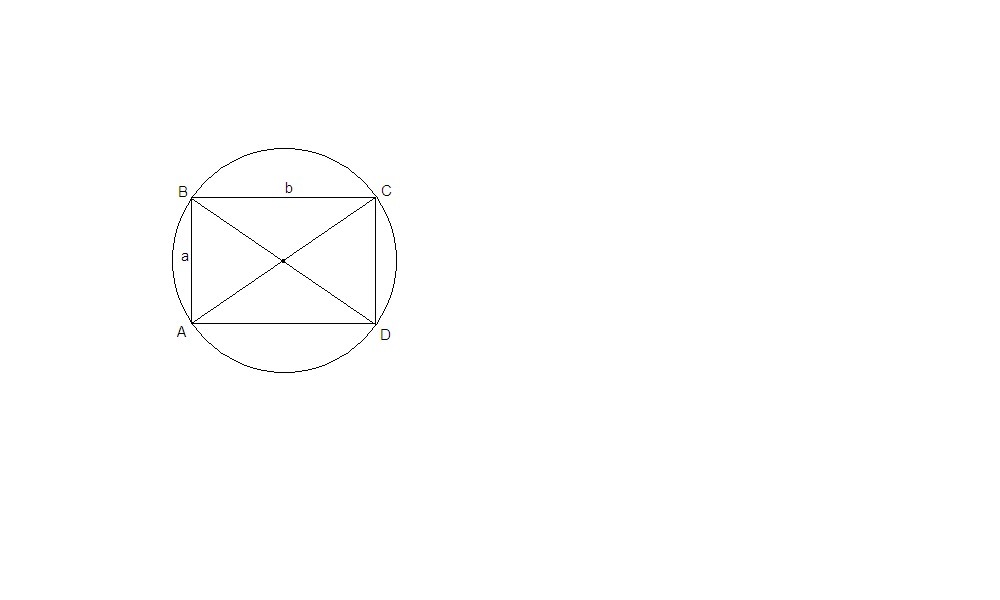
Центр окружности, описанной около прямоугольника, - точка пересечения диагоналей. Диагональ является его диаметром.
Радиус равен половине диагонали.
R = 10/2 = 5 см.

ΔАВС: по теореме Пифагора
a² + b² = 100
ab = 48                  площадь. 
Это система уравнений. Умножим второе уравнение на 2 и прибавим к первому:
a² + 2ab + b² = 196
2ab = 96                 

(a + b)² = 196
ab = 48

a + b = 16
ab = 48

a = 16 - b
b² - 16b + 48 = 0

По теореме Виета:
b = 8 см  или    b = 6 см
а = 6 см  или    а = 8 см
Стороны прямоугольника 6 см и 8 см