Предмет: Алгебра,
автор: babiymaks
Помогите решить Интеграл, СРОЧНО
Приложения:
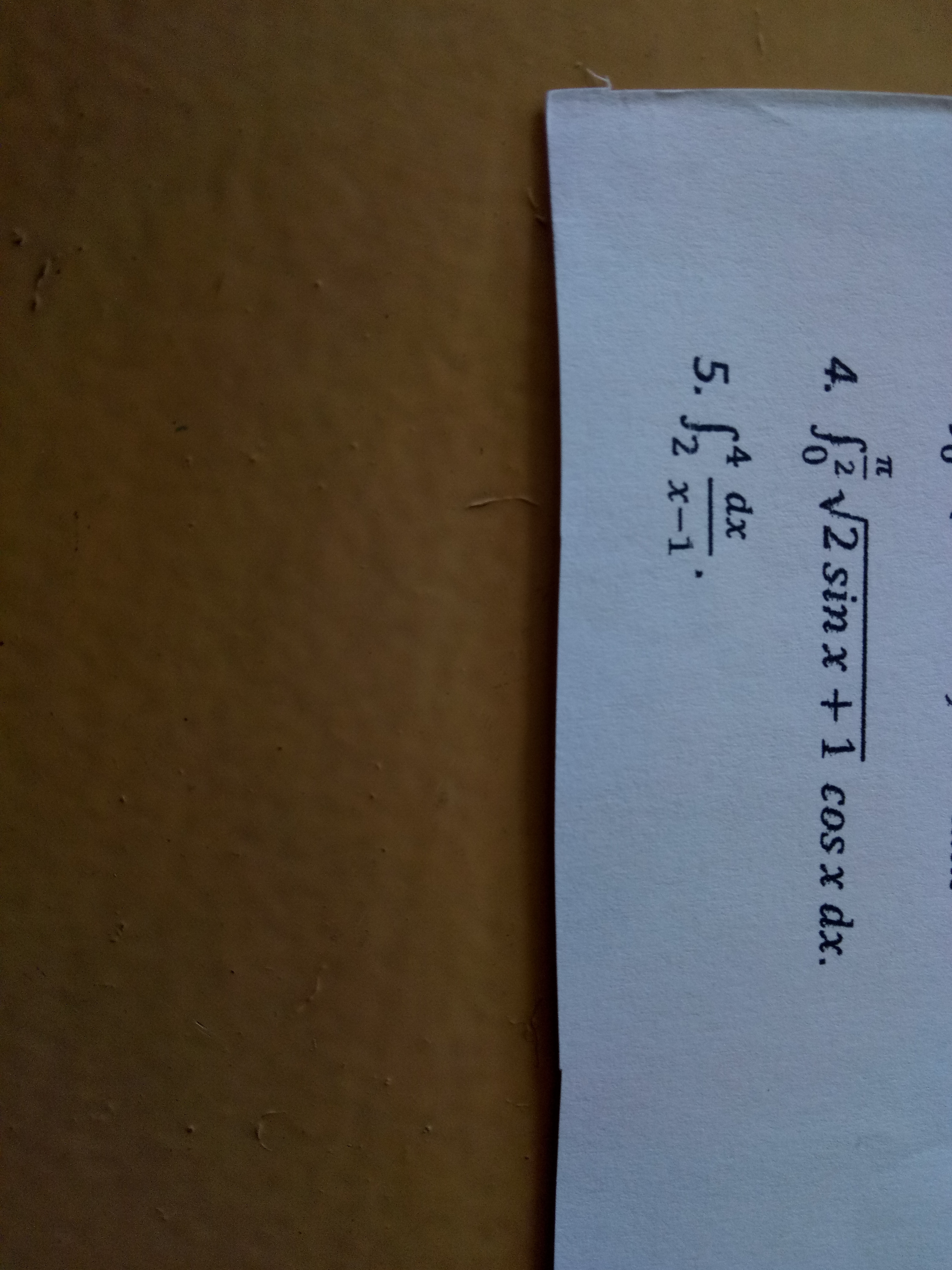
Ответы
Автор ответа:
0
4. Под знак дифференциала постепенно загоняем: сначала косинус, затем двойку и наконец единицу, т.е.  , чтобы получился табличный интеграл от степенной функции.
, чтобы получился табличный интеграл от степенной функции.


5.
5.
Похожие вопросы
Предмет: Математика,
автор: haletskyi25
Предмет: Физика,
автор: vikatop881
Предмет: Геометрия,
автор: sonaprodanova3790
Предмет: Математика,
автор: toliktolik1
Предмет: Литература,
автор: murlya