Предмет: Алгебра,
автор: KatrinB28
Показательное неравенство!Кто спец? Помогите, пожалуйста, решить!!!! №9
Приложения:
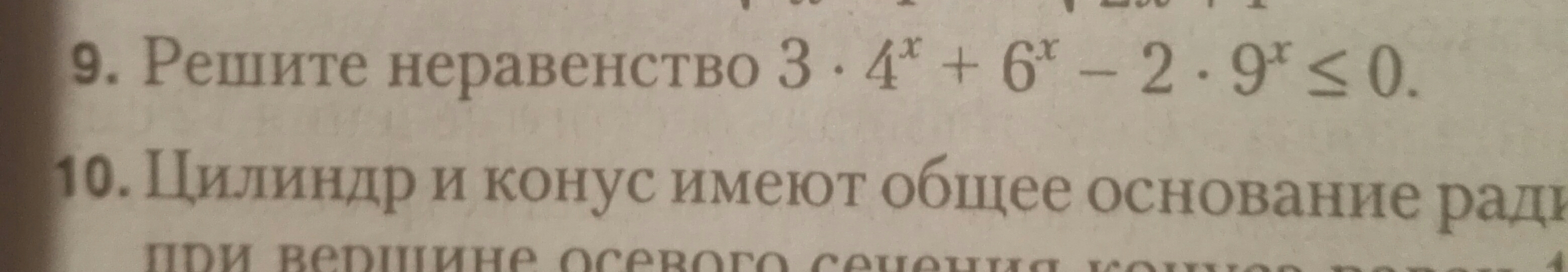
Ответы
Автор ответа:
0
Имеем: 
Преобразуем:
Разделим неравенство на . Т.к. оно больше нуля, то знак неравенства не изменится:
. Т.к. оно больше нуля, то знак неравенства не изменится:

Пусть , тогда
, тогда 
Умножим неравеество на t > 0, получим:
Решением данного неравенства является интервал: t ∈ [-1; 2/3]
Однако с учётом того, что t не меньше нуля: t ∈ [0; 2/3]
Делаем обратную замену:

Данное неравенство может выполняться только при x ≥ 1
Преобразуем:
Разделим неравенство на
Пусть
Умножим неравеество на t > 0, получим:
Решением данного неравенства является интервал: t ∈ [-1; 2/3]
Однако с учётом того, что t не меньше нуля: t ∈ [0; 2/3]
Делаем обратную замену:
Данное неравенство может выполняться только при x ≥ 1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: nastyapreobrazhenska
Предмет: Алгебра,
автор: sasharuslan2018
Предмет: Математика,
автор: marusy25032005
Предмет: Алгебра,
автор: Аноним