Question

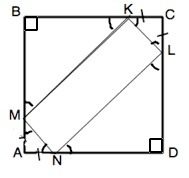
ABCD-квадрат,АМ=AN=CK=CL.Визначте вид чотирикутника MNKL

Answer 1

АВСD - Квадрат. АМ=AN=CK=CL. Укажите вид четырехугольника MNKL 
                      

∆ KCL=∆ MAN по двум сторонам и углу между ними. ⇒ MN=KL.

Стороны квадрата равны. Если от равных отрезков отнять по равной части, оставшиеся отрезки будут равны. ⇒

МВ=ВК=LD=ND. -⇒ Прямоугольные ∆ МВК=∆ LDN.

Четырехугольник MNKL – параллелограмм. 

Рассмотрим его углы на примере развернутого угла ВМА. 

Так как стороны параллелограмма отсекают от углов квадрата равнобедренные прямоугольные треугольники, ∠ВМК=∠NMА=45°. Поэтому ∠КМN=180°-2•45°=90°

Противолежащие углы параллелограмма равны ( можно доказать для каждого угла, что он равен 90°). Тогда сумма двух противолежащих  прямых углов равна 180°, и каждый из оставшихся также равен 90°. 

Следовательно, четырехугольник КМNL- прямоугольник.