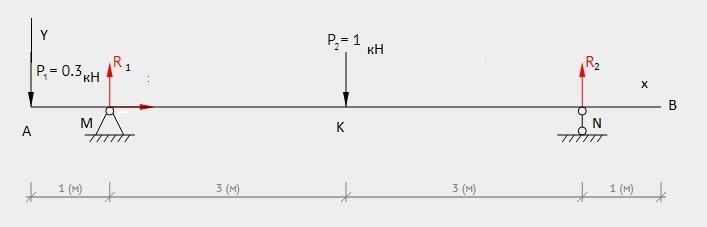
Балка длиной 8 м и массой 100 кг расположена горизонтально и покоится на двух опорах. AM = 1 м, MN = 6 м, NB = 1 м. На левом конце балки подвешен груз массой 30 кг. Определите силы, с которыми балка давит на опоры.
Ответы
Ответ:
R₁ = 0,85 кН
R₂ = 0,45 кН
Объяснение:
Дано:
L = 8 м
m₁ = 30 кг
m₂ = 100 кг
AM = 1 м
MN = 6 м
NB = 1 м
_________________
R₁ - ?
R₂ - ?
Сделаем чертеж. Проведем систему координат XY, укажем все силы - силы тяжести P₁ = m₁*g, P₂=m₂*, силы упругости (реакции балки) R₁ и R₂.
Найдем : P₁ = 30*10 = 300 Н = 0,3 кН
Р₂ = 100*10 = 1000 Н = 1 кН
В сопромате силы принято измерять в килоньютонах (кН).
У нас две неизвестных величины, значит, необходимо составит два уравнения равновесия.
Система находится в равновесии, если:
1) Сумма проекций всех сил на ось ОY равна нулю.
∑ Fx = - P₁ + R₁ - P₂ + R₂ = 0
-0,3 + R₁ - 1 + R₂ =0
R₁ + R₂ = 1,3 (1)
2)
Сумма моментов сил относительно оси равна нулю.
Условимся считать положительными моменты, если они направлены против часовой стрелки. Пусть ось вращения проходит через точку M.
∑ M = P₁*AM - P₂*MK + R₂ = 0
0,3*1 - 1*3 + R₂*6 = 0
R₂ = (3-0,3) / 6 = 0,45 кН
Из первого уравнения:
R₁ = 1,3 - 0,45 = 0,85 кН