Question

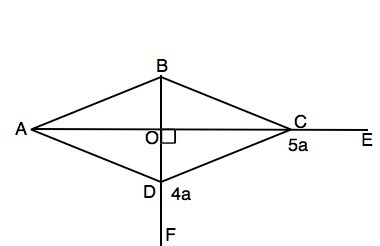
Сторона DC ромба ABCD образует с продолжениями его диагоналей BD и AC
углы FDC и ECD соответственно, которые относятся как 4:5. Найдите углы ромба

Answer 1

Примем коэффициент отношения данных углов равным а. 

Тогда ∠FDC=4a; ∠ECD=5a

Угол ОDF  развернутый, ⇒ угол ODC=180°-4a

Угол ОСЕ - развернутый ⇒ угол  ОСD=180°-5а.  

Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам. 

∆ DOC  прямоугольный. 

Сумма  острых углов прямоугольного треугольника =90°. 

180°-4а+180°-5а=90°

9а=270° ⇒

 а=30°

Угол ВDC=180°-4•30°=60°

Противолежащие углы ромба равны. 

Угол АВС=АDC=2•∠BDC=120° 

Сумма углов. прилежащих к одной стороне параллелограмма, равна 180°⇒

угол ВАD=BCD=180°-120°=60°