Предмет: Математика,
автор: DorogaDOMOY
пожалуйста!!!напишите решение.......
Найти общие интегралы уравнений и частные решения дифференциальных уравнений, удовлетворяющие начальным условиям:
Приложения:
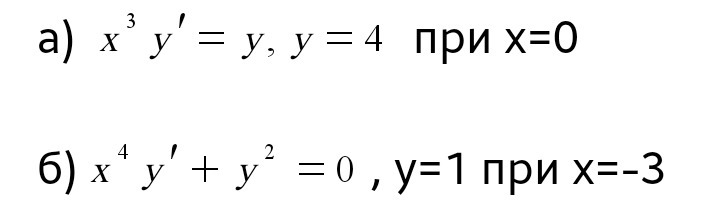
Ответы
Автор ответа:
0
Проверка:
Проверка:
Похожие вопросы
Предмет: Биология,
автор: live981
Предмет: Математика,
автор: voskalomaria65
Предмет: Английский язык,
автор: Salom0770
Предмет: Литература,
автор: МарийкаМария
Предмет: Математика,
автор: Эвелина111111