Предмет: Алгебра,
автор: likunya
Записать систему линейных уравнений, соответствующую уравнению в матричной форме: A*X=B, где X=(x y z) в столбик.
Решить полученную систему методом Крамера. матрицы обведены в таблице(см картинку)
Приложения:
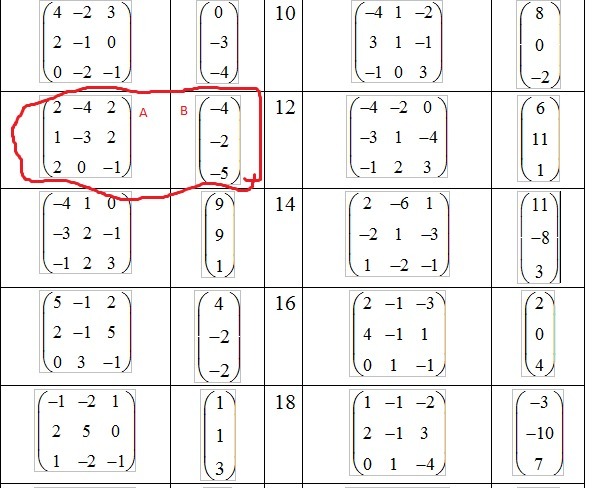
Ответы
Автор ответа:
0
Автор ответа:
0
здесь немножко подправил, посмотрите
Автор ответа:
0
да ничего страшного, все равно я не списываю не проверив вычисления)))
Автор ответа:
0
спасибо вам огромное
Автор ответа:
0
я просто сомневаюсь в своих решениях
Автор ответа:
0
если можете, решите еще задание
Похожие вопросы
Предмет: Литература,
автор: Nervers
Предмет: Другие предметы,
автор: gladyshevadinara
Предмет: Математика,
автор: zajcevdenis518
Предмет: Химия,
автор: 030520
Предмет: География,
автор: alinapeledina