Question

1)найдите площадь треугольника по трем сторонам: 5, 5, 6.
2)найдите стороны ромба зная что его диагонали относятся как 1:2, а площадь ромба равна 12 см. в квадрате.

Answer 1

1)
Прямоугольник равнобедренный, значит, его высота является медиано  и биссектрисой. Из прямоугольного треугольника АСВ:
AN=NB=6/2=3;
CN^2=CB^2-CB^2
CN^2=5^2-3^2=25-9=16
CN=4
Площадь S=1/2 * AB * CN = 1/2 * 6 * 4 = 12

2)
Пусть одна диагональ ромба равна х, тогда вторая 2х
Площадь ромба равна половине произведения диагоналей:
S = 1/2 * x * 2x
 1/2 * x * 2x = 12
x^2 = 12
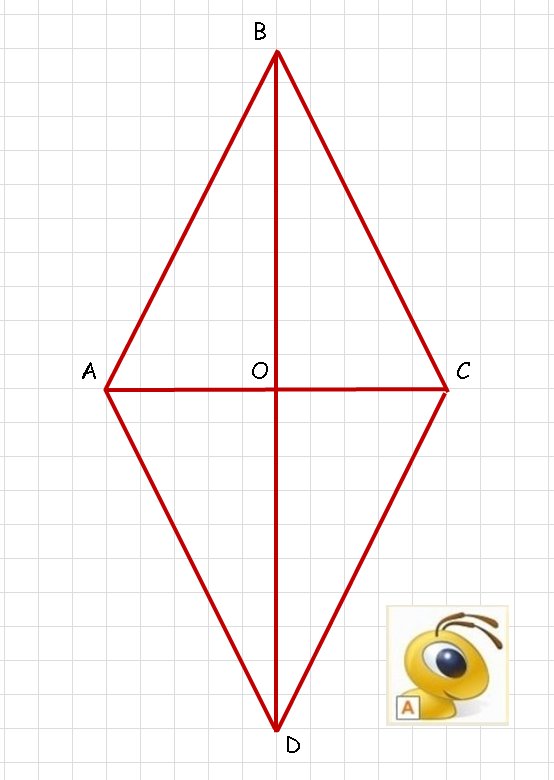
Рассмотрим прямоугольный треугольник AOB:
AO = x/2
OB = 2x/2 = x
AB^2 = AO^2+OB^2=(x/2)^2+x^2=3/2 x^2 = 3/2 * 12 = 18
$AB = sqrt{18}= 3sqrt{2}$