Question

доказать теорему если диагонали параллелограмма перпендикулярны , то этот параллелограмм - ромб

Answer 1

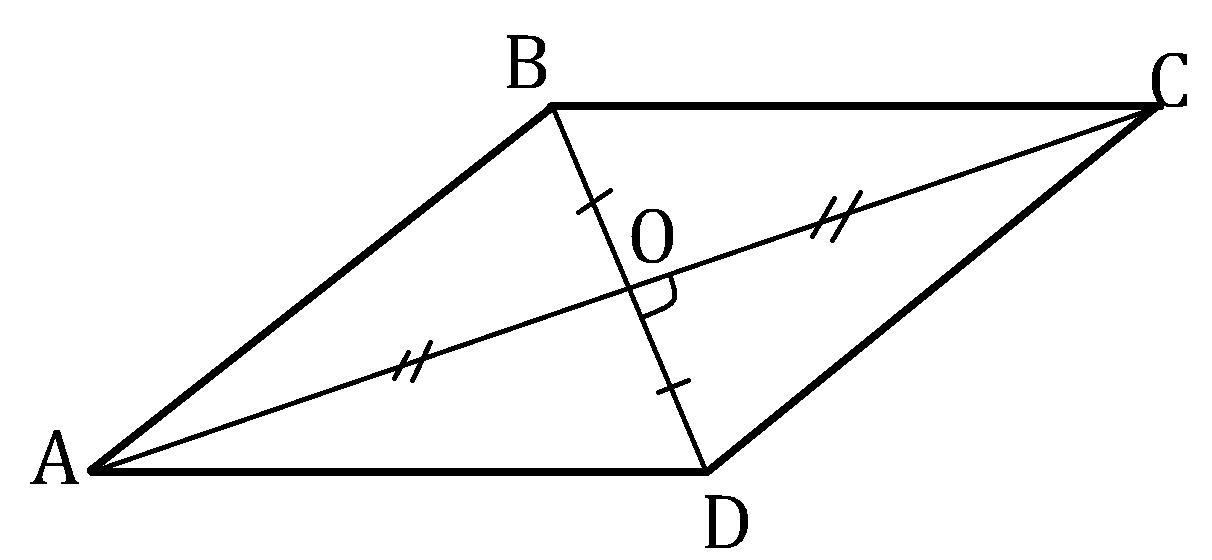
Дано: AB ║ CD; BC ║ DA; AC ⊥ BD.

Доказать: ABCD - ромб.

Решение:AC ∩ BD = O.

AO = OC и BO = OD т.к. диагонали параллелограмма делятся точкой пересечения на два равных отрезка.

Диагонали перпендикулярны, поэтому ΔABO, ΔBCO, ΔCDO и ΔDAO - прямоугольные, эти треугольники равны по двум катетам BO = OD и AO = OC. У равных треугольников соответственные стороны равны, поэтому их гипотенузы равны, а именно AB = BC = CD = DA. Параллелограмм, у которого все стороны равны, является ромбом, что и требовалось доказать.