Предмет: Математика,
автор: chapa00
Решите пожалуйста неравенство
Приложения:
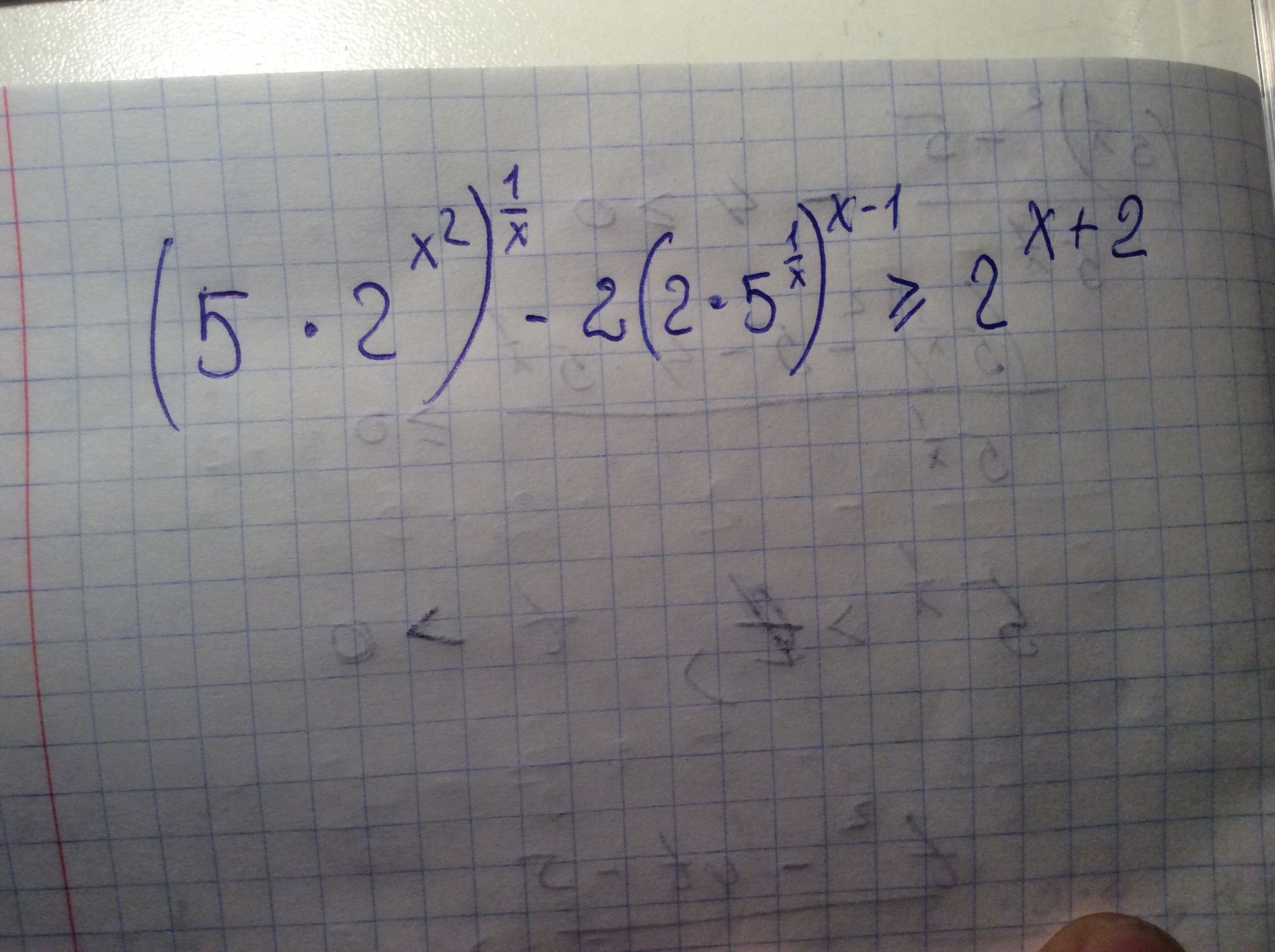
Ответы
Автор ответа:
0
Автор ответа:
0
Объясните, пожалуйста последнюю строчку - как вы получили 5^x^-1 - 5 >_ 0
Автор ответа:
0
5^x^-1 + 5 всегда положительно, следовательно, деля неравенство на это выражение, знак не поменяется
Похожие вопросы
Предмет: Биология,
автор: verakornienko947
Предмет: Литература,
автор: 2000618
Предмет: Математика,
автор: Ksenia0188
Предмет: Физика,
автор: Dimazab