Предмет: Геометрия,
автор: Алкадиеныч
Решить задачу на фотографии.
Приложения:

Ответы
Автор ответа:
0
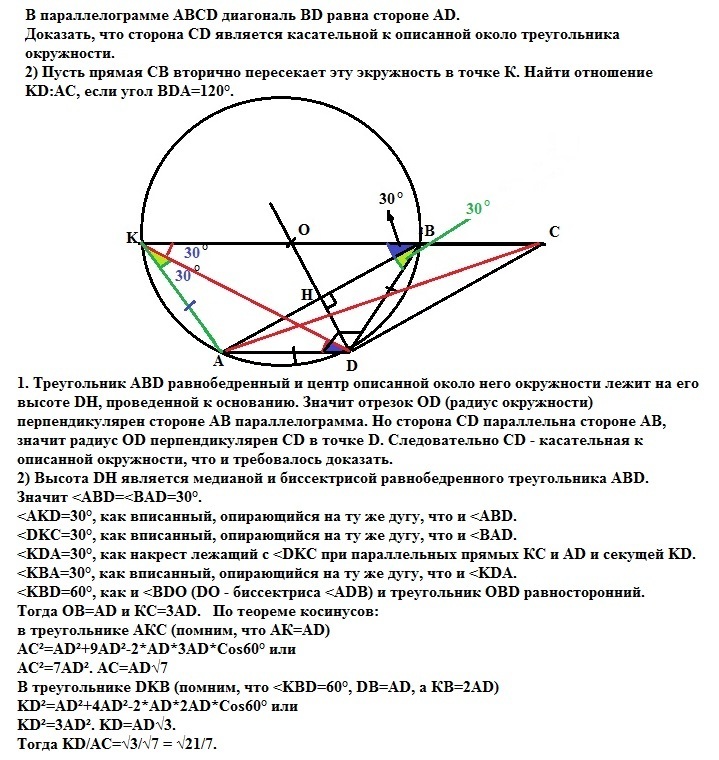
1. Треугольник ABD равнобедренный и центр описанной около него окружности лежит на его высоте DH, проведенной к основанию.
Значит отрезок OD (радиус окружности) перпендикулярен стороне АВ параллелограмма. Но сторона CD параллельна стороне АВ, значит радиус OD перпендикулярен CD в точке D.
Следовательно CD - касательная к описанной окружности, что и требовалось доказать.
2) Высота DH является медианой и биссектрисой равнобедренного треугольника ABD. Значит <ABD=<BAD=30°.
<AKD=30°, как вписанный, опирающийся на ту же дугу, что и <ABD.
<DKC=30°, как вписанный, опирающийся на ту же дугу, что и <BAD.
<KDA=30°, как накрест лежащий с <DKC при параллельных прямых КС и AD и секущей KD.
<KBA=30°, как вписанный, опирающийся на ту же дугу, что и <KDA.
<KBD=60°, как и <BDO (DO - биссектриса <ADB) и треугольник ОВD равносторонний.
Тогда ОВ=AD и КС=3AD. Тогда по теореме косинусов:
в треугольнике АКС (помним, что АК=АD)
АС²=AD²+9AD²-2*AD*3AD*Cos60° или
АС²=7AD². AC=AD√7
В треугольнике DKB (помним, что <KBD=60°, DB=АD, а КВ=2AD)
KD²=AD²+4AD²-2*AD*2AD*Cos60° или
KD²=3AD². KD=AD√3.
Тогда KD/AC=√3/√7 = √21/7.
Значит отрезок OD (радиус окружности) перпендикулярен стороне АВ параллелограмма. Но сторона CD параллельна стороне АВ, значит радиус OD перпендикулярен CD в точке D.
Следовательно CD - касательная к описанной окружности, что и требовалось доказать.
2) Высота DH является медианой и биссектрисой равнобедренного треугольника ABD. Значит <ABD=<BAD=30°.
<AKD=30°, как вписанный, опирающийся на ту же дугу, что и <ABD.
<DKC=30°, как вписанный, опирающийся на ту же дугу, что и <BAD.
<KDA=30°, как накрест лежащий с <DKC при параллельных прямых КС и AD и секущей KD.
<KBA=30°, как вписанный, опирающийся на ту же дугу, что и <KDA.
<KBD=60°, как и <BDO (DO - биссектриса <ADB) и треугольник ОВD равносторонний.
Тогда ОВ=AD и КС=3AD. Тогда по теореме косинусов:
в треугольнике АКС (помним, что АК=АD)
АС²=AD²+9AD²-2*AD*3AD*Cos60° или
АС²=7AD². AC=AD√7
В треугольнике DKB (помним, что <KBD=60°, DB=АD, а КВ=2AD)
KD²=AD²+4AD²-2*AD*2AD*Cos60° или
KD²=3AD². KD=AD√3.
Тогда KD/AC=√3/√7 = √21/7.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: PERVINHUSEYNOVA86
Предмет: Химия,
автор: Efimochka
Предмет: История,
автор: azatshayakhmetov
Предмет: Математика,
автор: di102015
Предмет: Физика,
автор: алихан6