Предмет: Алгебра,
автор: денис483
Помогите решить пожалуйста
Приложения:
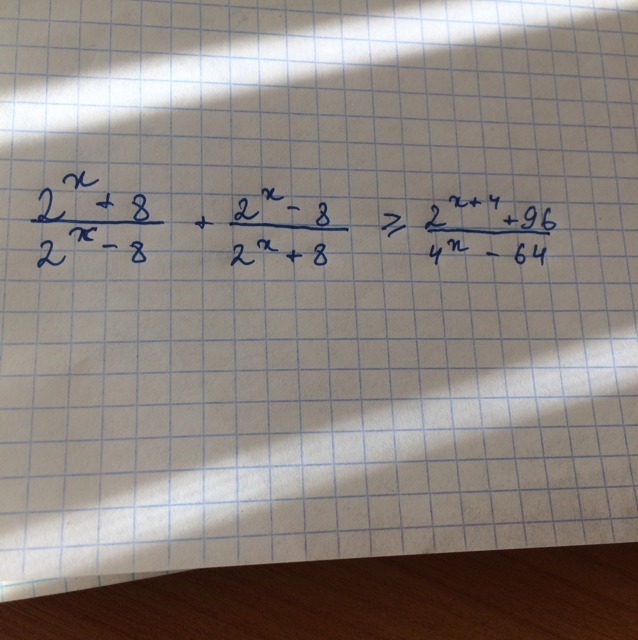
Ответы
Автор ответа:
0
Чтобы упростить себе жизнь сделаем замену у=2ˣ, y>0, тогда 4ˣ=(2²)ˣ=(2ˣ)²=y²
Получаем неравенство

Решаем


Это дробь равна нулю только когда ее числитель равен нулю, то есть в точке y=4
Вспоминаем, что y по условию всегда положительный, значит у+8 всегда >0.
Таким образом дробь может принимать отрицателтные значения только когда y-8 <0, то есть у <8
Значит y∈ [4;4]∪(8;+∞)
x∈[2;2]∪(3;+∞)
Получаем неравенство
Решаем
Это дробь равна нулю только когда ее числитель равен нулю, то есть в точке y=4
Вспоминаем, что y по условию всегда положительный, значит у+8 всегда >0.
Таким образом дробь может принимать отрицателтные значения только когда y-8 <0, то есть у <8
Значит y∈ [4;4]∪(8;+∞)
x∈[2;2]∪(3;+∞)
Похожие вопросы
Предмет: Химия,
автор: kirillsatuhin809
Предмет: Химия,
автор: Zafkiel35
Предмет: Литература,
автор: aser08dwrftj
Предмет: История,
автор: мася04
Предмет: Математика,
автор: Аноним