Предмет: Алгебра,
автор: suslr1999
Решите пожалуйста 3 пример, буду благодарен.
Приложения:
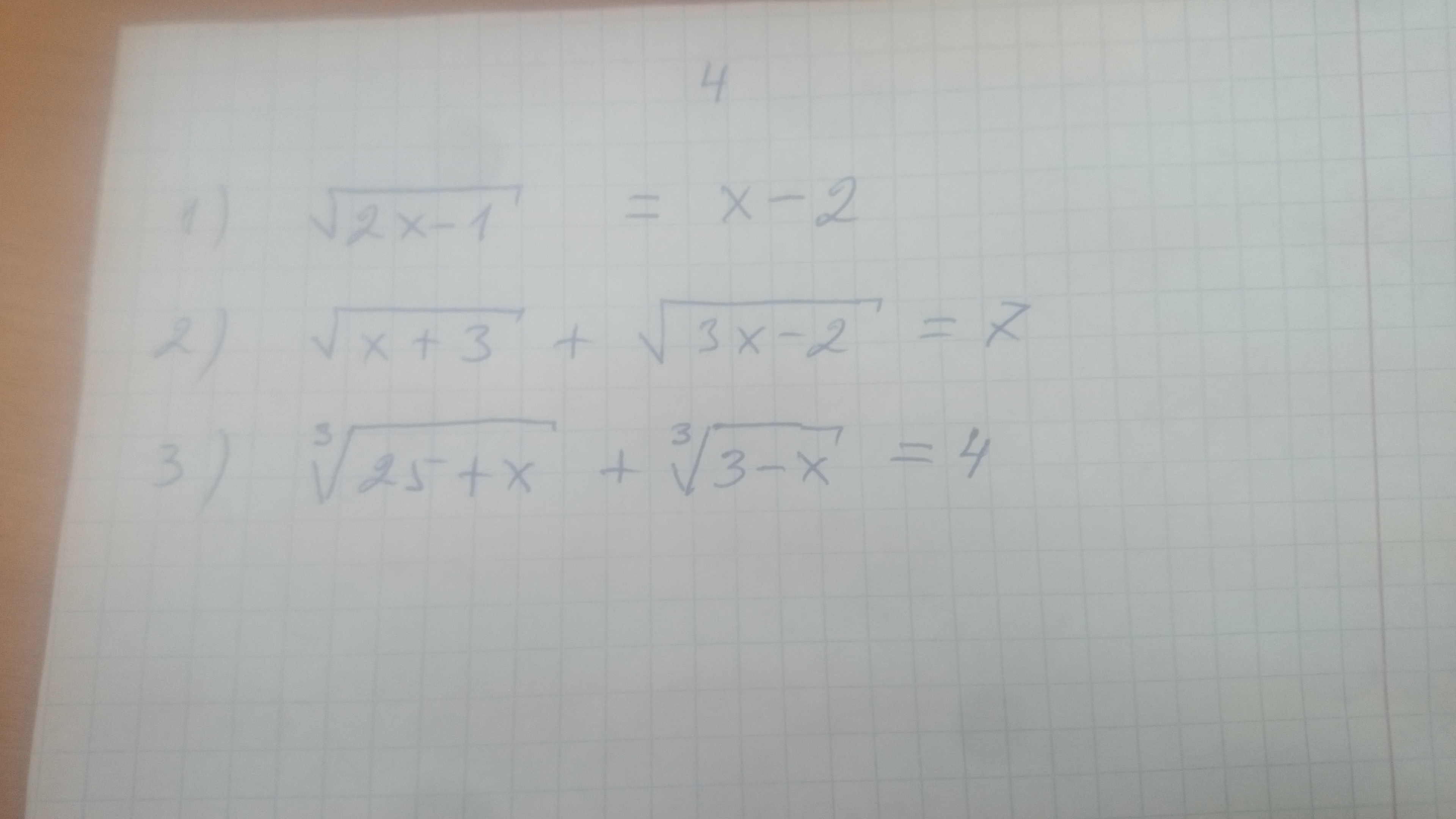
Ответы
Автор ответа:
0
Можно конечно возвезти в куб, но я предлагаю идею по-проще.
взять производную левой части, найти точку глобального максимума, если таковой имеется, а таковой имеется.
производная левой части = 1/(3(x+25)^(2/3))+1/(3(3-x)^(2/3))
Нас необходимо, чтобы знаменатели были равны. Получаем корень: x=11
проведя числовую линию, отметив точку -11, получаем, что при х<-11 график возрастает, а x>=-11 - убывает. следовательно -11 - точка глобального максимума. а y(11) = 2(14)^(2/3), что больше 4.
значит в нашем уравнении всего два корня. которые можно спокойно найти
нам, конечно, желательно, чтобы подкоренное выражение было кубом какого-то числа
Наши ответы: x=2 or x=-24
взять производную левой части, найти точку глобального максимума, если таковой имеется, а таковой имеется.
производная левой части = 1/(3(x+25)^(2/3))+1/(3(3-x)^(2/3))
Нас необходимо, чтобы знаменатели были равны. Получаем корень: x=11
проведя числовую линию, отметив точку -11, получаем, что при х<-11 график возрастает, а x>=-11 - убывает. следовательно -11 - точка глобального максимума. а y(11) = 2(14)^(2/3), что больше 4.
значит в нашем уравнении всего два корня. которые можно спокойно найти
нам, конечно, желательно, чтобы подкоренное выражение было кубом какого-то числа
Наши ответы: x=2 or x=-24
Автор ответа:
0
Таковая*
Автор ответа:
0
И, кстати, я ошибся в знаки в производной. второе слагаемое берется со знаком минус.
Автор ответа:
0
в знаке*
Похожие вопросы
Предмет: География,
автор: alina533182827
Предмет: История,
автор: trend4ik1254
Предмет: Английский язык,
автор: eldossagadiev603
Предмет: Физика,
автор: avilika
Предмет: Математика,
автор: ilovebooze